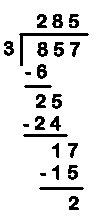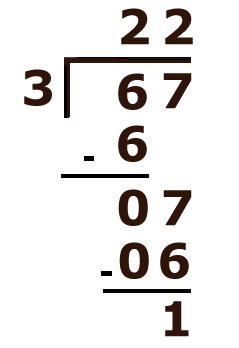| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
LES TABLES DE MULTIPLICATIONS
Autrefois, on disait: "L'apprentissage des tables s'appuie sur trois types de mémoires (auditive, visuelle, mécanique)". Neuromythe ? Pas si sûr. Cela voulait dire surtout qu'il fallait ne négliger aucun sens.
Il suffit de parcourir les livres anciens pour se rendre compte qu'il y avait différentes façons d'apprendre et de mémoriser les tables de multiplications. Toutes les méthodes ne se valent pas. Mais que doit-on mémoriser ? Le son, résonance du résultat ou l'algorithme complet qui mène au résultat ? Le réflexe ou l'automatisme ? Ne comptez surtout pas sur les livres en service à l'école française pour initier correctement les enfants aux tables de multiplication et surtout à les mémoriser de façon pérenne. Les décompositions multiplicatives, les schémas, les algorithmes, tout le monde les ignore. Ne comptez pas non plus sur Internet, c'est le café du commerce... On s'ingénie à fabriquer des réflexes en utilisant des trucs souvent éloignés d'un raisonnement mathématique. Personne ne sait plus construire des automatismes qui peuvent être au départ laborieux, mais qui finissent par devenir spontanés. Cela n’exclut pas, bien sûr, de les apprendre par cœur. Mais l’enfant doit, d’abord, en avoir compris le sens. Excellent, le livre de Singapour de CE2 ! Il suffit de l'ouvrir, pour constater qu'à Singapour on mémorise, d'abord, des algorithmes calculatoires résumés dans des schémas. C'est aussi énorme que le nez au milieu de la figure. Cette méthode semble issue de la recherche française des années 60, revisitée, celle qui était publiée dans la revue syndicale l'Ecole libératrice. Exemple:
 Qu'en pense-t-on à Singapour ? Qu'en pense-t-on à Singapour ?
Learning the times tables is key to mastering primary school math, as memorisation of the tables support mathematical learning and understanding of multiplication and division. These concepts form the foundation to our mental arithmetic, as well as estimation skills. Research has shown that children become more confident and open to learning new concepts once they have mastered the times tables.
L'apprentissage des tables de multiplication est la clé de la maîtrise des mathématiques de l'école primaire, car la mémorisation des tables favorise l'apprentissage mathématique et la compréhension de la multiplication et de la division. Ces concepts forment la base de notre arithmétique mentale, ainsi que des compétences d'estimation.
Bien entendu, il s'agit de la recherche à Singapour, pas de la recherche pédagogique française, américaine, occidentale...La recherche a montré que les enfants deviennent plus confiants et ouverts à l'apprentissage de nouveaux concepts une fois qu'ils ont maîtrisé les tables de multiplication. Ce qui est impressionnant, quand on compare les livres de Singapour et les livres français, c'est le nombre de pages consacrées aux tables de multiplication. En France, ce travail est bâclé dans tous les livres, alors qu'à Singapour, on y consacre deux chapitres complets et les leçons y sont admirablement illustrées. Comprendre avant d'apprendre. C'est cette étape primordiale, essentielle, qui a été oubliée en France. Peut-on aimer les mathématiques si on ne comprend pas des choses aussi simples !
IMPORTANT !!!
Le livre de CE2 de Singapour dont je fais l'éloge est celui préfacé par le grand mathématicien Laurent Lafforgue (Médaille Fields 2002 et grand spécialiste de la théorie des nombres). Une nouvelle version vient de paraître, une traduction américanisée qui ne tient aucun compte des particularités de la langue française. Là, je rejoins Rémi Brissiaud. Avec cette nouvelle collection de cette méthode dite de Singapour, contradictoire à la précédente, c'est la pédagogie américaine qui envahit la France. On fait beaucoup d'expérimentations aux USA, mais où sont les progrès ? Les USA occupent la 37e place au classement Pisa 2019, en mathématiques, avec 478 pts, loin derrière la France qui n'est pourtant pas brillante (25e, 495 pts) et surtout de Singapour (549 pts) ou de la Chine (555 pts). À mes amis américains, je conseillerai de remplacer leur traditionnelle droite numérique, par le mètre pliant.
Je propose à tous de réfléchir, à quoi peut bien servir la droite numérique américaine : Certainement pas à bien calculer. Priorité, d’abord, au calcul-dénombrement et aux images mentales (nombres cardinaux) ! Et sans point de repère sur une droite, comment peut-on s’orienter (nombres ordinaux) ? Dans la numération décimale, les nombres terminés par un zéro, deux zéros, trois zéros... sont des repères naturels. Les laudateurs de la droite numérique américaine ne savent pas ce qu’est un nombre. Je le démontre plus bas : Il n’y a pas d’espace entre deux nombres consécutifs. Il y a des espaces entre les numéros ! Tous les travaux de la recherche pédagogique américaine et de ceux qui s'en réclament sont influencés, perturbés, par cette grossière erreur initiale. Lorsqu'on a trouvé une méthode qui fonctionne, on s'y tient, on la fignole, on l'adapte à ses élèves, on la perfectionne, tout en sachant qu'il n'y a pas, malheureusement, de méthode miracle. Mais si vous en connaissez une meilleure que la mienne, merci de me la faire connaître.
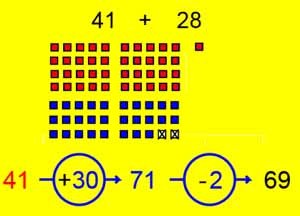
Comme on manipule élément par élément, des lignes incomplètes peuvent apparaître, suivant le problème posé. Cela va aider l'enfant à comprendre la division euclidienne. (encadrement d'un nombre compris entre deux bornes - donc repères spatiaux). Net avantage, par rapport aux méthodes des croisements de baguettes (Chine) ou des rectangles quadrillés (Singapour) qui ne permettent, que de mettre en évidence, la commutativité de la multiplication et la permutation, diviseur quotient, quand le reste de la division est nul. Pour une conceptualisation complète des nombres, il est important de savoir que les nombres à retenir pour la table par 7, par exemple, ne sont que des repères dans la suite, des bornes d'intervalles.
ou mieux (Personnellement, je préfère la ligne brisée à la ligne droite.)

Tout un symbole La calamité des premiers pas en mathématiques. L'enfant est obligé de mémoriser par cœur des relations numériques aussi idiotes que les tables d'addition !
La disposition des nombres préconisée par la méthode de Singapour recommandée par Laurent Lafforgue est astucieuse. On voit très bien en bout de ligne, ce que l'on appelait autrefois les gares des dizaines. (10-20-30-40-etc ...)
On passe
Autrefois, c'est ce calcul que l'on faisait faire pour établir la liste des multiples de 7. Il ne nous serait jamais venu à l'idée de faire du comptage-numérotage. Comment voulez-vous qu'un enfant puisse trouver des repères sur cette droite numérotée américaine ? Pourquoi ne pas utiliser une ligne brisée pour représenter la suite des nombres ? Le tableau comprenant les gares des dizaines, permet d'aller bien plus loin que la table de multiplication, de jouer avec les nombres. On peut observer une disposition géométrique des nombres multiples de 7. Dans la suite de nombres matérialisée par la ligne (14 ... 98), quel sera le multiple suivant ? Cette suite de nombres est géniale: Elle utilise les compléments à 10 et les décompositions additives du nombre 7 (de 6 , 8 ou 9 pour les autres tables difficiles à mémoriser). Là, on joue avec les nombres. On ne numérote pas. Je ne connaissais pas cette méthode. On a toujours quelque chose à apprendre. Mais les "experts" français, eux, ils savent tout. Ils n'ont rien à apprendre des autres. Ils osent même faire la leçon aux pédagogues singapouriens de Singapour, malgré les" brillants" résultats des élèves français. J'ai appris la file ordinale des 100 premiers nombres en pliant et dépliant un mètre de dix brins gradués ( en métal: 10 fois 10 cm). La largeur de chaque brin mesurait 1 cm. On comptait des cm2, donc des carrés. Ne pas confondre avec le double-mètre des charpentiers en bois (10 brins de 20 cm). J'ai mes repères (les gares des dizaines) et ils me servent pour retrouver les cardinaux, la numération décimale,... et faire toutes sortes de calculs par décompositions de nombres. La file numérotée américaine, rectiligne, infinie, ne le permet pas.
Mon mètre pliant à l'avantage de faire coexister le comptage-numérotage et le comptage-dénombrement. On numérote en lisant les numéros (bornes d'intervalles) et on dénombre en comptant les carrés (les intervalles). Je me servais du mètre pliant après avoir fait étudier les nombres inférieurs à 20 à l'aide du domino double cinq. Pour les petits nombres, on a une meilleure représentation spatiale dans un espace en deux dimensions que sur une simple ligne, surtout droite. Et on mémorise plus facilement des ensembles d'éléments de forme ronde.
On a la même coexistence sur le cadran d'une horloge (intervalles et bornes d'intervalles sur une file numérique circulaire) Voir une page que j'avais écrite il y a déjà plusieurs années :  L'horloge et les nombres L'horloge et les nombres
Là je démontre qu’il n’y a pas d’espace entre deux nombres consécutifs.
Il ne suffit pas de dénoncer la nocivité de la droite numérique américaine comme le fait, à juste titre et brillamment, Rémi Brissiaud.  Voir. Voir. Il faut prouver sa nuisance. On peut enseigner au Collège de France et confondre numéro et nombre , et ce qui est plus grave, intervalle et borne d'intervalle. Il faut apprendre à combiner l'ordinal et le cardinal. Vous découvrirez ma preuve finale, incontestable, dans la chanson de Berthe Sylva. Rémi Brissiaud montre surtout une incompétence pédagogique. Moi, je montre une incompétence scientifique en une théorie élémentaire des nombres.
C'est le 7e ensemble de carrés. Il comporte 7 éléments. Dès qu'on franchit la ligne on entame le nombre suivant. Voyez-vous un quelconque espace ? Sur la suite de Singapour, l'étiquette placée au centre du 7e carré semble ne désigner qu'un seul carré: c'est une position ambigüe.
Le nombre cardinal désigne tous les éléments d’un ensemble.
Moi, je préfère donc le mètre pliant à dix brins qui a le mérite de distinguer les ordinaux des cardinaux, puis de pouvoir les combiner pour calculer en dénombrant.Le nombre ordinal ne désigne qu’un seul élément de cet ensemble, le dernier compté. C’est le numéro affiché qui va permettre de combiner le nombre cardinal et le nombre ordinal. Lorsque l’enfant aura compris cette subtilité, il aura fait un grand progrès en mathématiques. C'est la voie vers l'abstraction véritable. Dans un cours au collège de France, lorsque l’orateur place le curseur à un endroit précis, il ne peut s’agir que d’un nombre ordinal parce que le cardinal c’est le nombre d'éléments de l'ensemble depuis le début de la file. J’espère que ce n’est qu’une erreur de langage. Il aurait donc fallu utiliser le mot numéro. Un instituteur sait par expérience, qu'en mathématiques, avec des enfants, il faut être méticuleux et utiliser un vocabulaire précis. Et chaque chose doit être à sa place. Il faut éviter de faire perdre leurs repères spatiaux. Malheureusement, j'ai perdu ma fiche explicative de l'école libératrice. C'était tout aussi génial que la représentation ci-dessus du premier livre français traduit de la méthode de Singapour. Je ne suis pas un spécialiste du CP, de l'apprentissage des 100 premiers nombres. À la page l'horloge et les nombres, je raconte une expérience familiale. Mais dans ma famille, nous ne sommes pas trop mauvais en mathématiques... Voir la résolution de problèmes de certif. (Trois générations) Je ne me permettrai pas d'aller porter la contradiction à des collègues qui ont consacré toute leur vie au CP. Ils ont sûrement trouvé des solutions pour faire progresser leurs élèves. Mais je sais comment enseigner les tables de multiplication et de division dans notre chère langue de Molière. Et que doit savoir un enfant avant d'entrer à l'école primaire, au CP ? Pour savoir ce qui est réellement recommandé à Singapour, le mieux est d'aller directement sur place et de faire la traduction soi-même. C'est possible grâce à Internet. Le nom de domaine est bien SG. Nous sommes donc à Singapour. Tirez vos conclusions vous-mêmes... Quant à moi, je remarque qu'il n'y a pas de pré-requis pour entrer au CP, seulement, des attendus. La qualité de l'enseignement des premières années de l'école de Singapour fera que d'éventuels retards ou erreurs seront facilement rattrapés. C'est ce qu'on faisait encore en France dans les années 1980. Cela tient en un seul mot, inhibition. (Olivier Houdé) Il y a eu plusieurs raisons à l'effondrement des performances des petits Français en calcul. Prétendre qu'enseigner le seul comptage-dénombrement additif en maternelle permettra de rattraper le retard français, c'est une forfanterie. Pour tout savoir (Ministry of Education SINGAPORE):
Alors, qui est en retard par rapport à l’autre ? Le moins que l'on puisse dire: "Ce n'est pas la pédagogie du 19e siècle !" Les pédagogues français racontent n’importe quoi pour dénigrer la pédagogie de Singapour. Pour eux, c’est forcément mauvais car elle contredit leurs pratiques. « Qui veut noyer son chien, l'accuse de la rage. » Moi, simple et obscur instituteur, j’aimerais bien pouvoir échanger directement avec mes pairs singapouriens. J’aurais beaucoup à apprendre d’eux, bien plus que des personnes qui ne sont jamais devant les élèves. En étudiant attentivement ce curriculum, on ne peut que constater que nous avons des années-lumière de retard sur la pédagogie de Singapour !
Il serait peut-être temps que les pédagogues français abandonnent l’idée qu’ils seraient les meilleurs du monde !
Je constate, que contrairement à la dernière « méthode de Singapour franco-américaine », on ne parle de droite numérique, qu’à la troisième année d’enseignement, c’est à dire au CE2. Apprendre ses tables de multiplication, ce n'est pas seulement pouvoir les sortir bêtement par des réflexes. La méthode de l'école libératrice et celle de Singapour permettent de structurer l'apprentissage par cœur des tables de multiplication et de division. Jean Pierre Serre est un génie des mathématiques, l'un des plus grands mathématiciens du 20e siècle et du début de ce 21e. Le commun des mortels aura besoin de l'aide du maître qui lui laissera l'illusion qu'il a trouvé tout seul un algorithme, pour mémoriser une ligne de table. Mes programmes informatiques permettent de fixer les tables, mais surtout de graver en mémoire l'algorithme car à chaque opération, avec mes programmes, on visualise des quadrillages, des schémas rappelant les manipulations: La géométrie au service de l'arithmétique. Et, ce qui était rébarbatif, devient un jeu. Un enfant est bien plus concentré devant un écran, il n'a pas la pression ressentie à l'oral par le procédé Lamartinière. J'ai pu, par le passé, constater un gain de temps appréciable dans les apprentissages mécaniques. L'ordinateur est un répétiteur infatigable. C'est un entraînement qui favorise l'automatisation des procédures préalablement apprises.
Je demande à apprécier la démarche. Contrairement à tous les programmes que l’on peut trouver sur Internet, je ne me contente pas de noter la réponse (bon-mal). Je donne la réponse exacte, mais je permets aussi de vérifier la réponse par l’affichage de schémas qui rappellent comment on a essayé de les comprendre en manipulant. Je favorise l'installation d'automatismes. Je ne cherche pas à provoquer un réflexe. Je précise que tous mes programmes informatiques fonctionnent aussi bien sous Windows que sous Linux. Ils sont écrits en langage PHP ou JavaScript. Je fournirai le code source PHP à celui qui m'en fera la demande. Le code Javascript apparaît en clair dans les fichiers HTM. PHP permet de garder en mémoire les réponses des enfants dans des tables MySql ou des fichiers textes. Chacun pourra les modifier comme bon lui semblera pour une meilleure efficacité dans sa classe.
IMPORTANT: 2 x 9 =18 peut être lu 2 multiplié par 9 égale 18 ou 9 fois 2 dix-huit.
2+2+2+2+2+2+2+2+2=18 doit être lu deux plus deux plus deux plus deux plus deux plus deux plus deux plus deux plus deux égale dix-huit. Cette longue addidion peut être remplacée par la multiplication deux multiplié par neuf égale dix-huit. soit 2 x 9 = 18 On a lu deux, neuf fois. En mathématiques modernes on dira que l'opérateur est x9 (multiplier par 9 ou 9 fois). Avant 1970, c'était plus clair: 9 fois 2 œufs s'écrivait 2 œufs X 9 = 18 œufs. Mais on aurait fait remarquer qu'il est plus rapide de calculer le résultat en changeant l'ordre des facteurs : 2 fois 9 font 18. En aucun cas on ne doit donc lire 2 fois 9 égale dix-huit. C'est une entrave à la compréhension des problèmes liés à cause des repères spatiaux. Pour un enfant, chaque chose doit être à sa place. La commutativité sert surtout la rapidité des calculs. Et cela conduira à reporter à beaucoup trop tard l'apprentissage de la division.
Comment, un enfant qui commence tout juste à apprendre ses tables, peut-il comprendre, qu'il y a la même écriture, la même lecture, pour deux problèmes différents ?
Il y a un gros souci de repérage spatial.
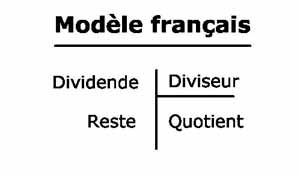
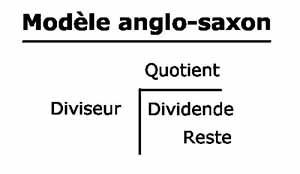
La division euclidienne n'est pas commutative. 17 divisé par 7 égale 2 et il reste 3. Mais 17 divisé par 2 égale 8 et il reste 1. Mais on peut toujours permuter diviseur et quotient quand le reste est nul ou inférieur au quotient.(Voir les travaux de John O'Keefe, May-Britt et Edvard Moser: "Le GPS neuronal"). C'est la preuve de la division qui va éclairer le sens de l'opération dans le problème posé, grâce à la commutativité de la multiplication bien comprise.
Extrait du livre du maître : math et calcul CE2 (R. Eiller)
Commutativité
La multiplication des entiers naturels est commutative, c'est-à-dire : Quels que soient les nombres naturels a et b on a : a x b = b x a. Remarques :II convient de lever une ambiguïté concernant cette propriété. En effet, les maîtres disent fréquemment que « 3 fois 4 » et « 4 fois 3 » « ce n'est pas la même chose ». En fait, il est évident que, lorsqu'on considère 3 rangées de 4 personnes et 4 rangées de 3 personnes, les « situations » ne sont pas les « mêmes ». Si on achète 3 objets à 4 F la pièce ou 4 objets à 3 F la pièce, les « situations » ne sont pas non plus les « mêmes ». Mais ce qu'il faut bien comprendre, c'est qu'au niveau des nombres on a l'égalité 4x3=3x4 (précisément à cause de la commutativité). Mais avec la création du corps des professeurs des écoles, les maîtres n'ont plus droit à la parole et les apprentis sorciers peuvent faire ce qu'ils veulent. Et ils mettent la charrue avant les bœufs. Certains n'hésitent pas à faire utiliser la calculatrice, début de CE2, à un enfant, qui rencontre 9 fois 8 pour la première fois.
« L'enfant veut réussir. Il ne veut pas nécessairement comprendre. Alors on le voit à de nombreux exemples: C'est l'enfant d'école primaire qui préfère utiliser la calculette plutôt que de comprendre le phénomène de la division. Et en fait, il a d'une certaine manière raison.
Et on se demande pourquoi tant de gens détestent les mathématiques !On sait le résultat de la division sans avoir à apprendre la division, si on utilise la calculette. » Faire réussir sans comprendre, pas le summum de la pédagogie.
À cet éminent pédagogue bien connu, qui n'a pas dû enseigner beaucoup dans les petites classes, je proposerais bien le problème suivant :
Le maître partage une tablette de chocolat de 4 rangs de 8 carreaux entre les 7 élèves de son CE2. Combien de carreaux chaque élève pourra-t-il déguster ? Combien en restera-t-il au maître ? La calculette (qui n'a que 4 opérateurs) affiche la réponse suivante : 4.571428571428571 La calculette ne donne pas la réponse adéquate, et pourtant, enfants et maître devraient être également satisfaits. (4 carreaux pour tout le monde) Je considère que c'est une faute pédagogique monumentale que de faire utiliser une calculatrice par un enfant qui ne maîtrise pas l'algorithme opératoire, donc qui ne connaît pas les différents sens des opérateurs, et c'est l'inciter à une paresse intellectuelle. Avant même d'utiliser la calculatrice pour vérifier une opération, il faudrait apprendre aux enfants à la vérifier d'abord par le calcul. La vérification de la soustraction et de la division, tout en décelant les erreurs, éclaire le sens des problèmes posés et pour la multiplication, elle permet de comprendre la commutativité. Faire réussir sans comprendre, c'est favoriser l'entrée dans la société de consommation. Nul besoin de soulever le capot de la voiture pour savoir la conduire. Le progrès selon cette personne adulée par une majorité de formateurs qui sévissent aujourd’hui. La lecture du programme de Singapour cité plus haut, m’apprend que ce n’est qu’à la cinquième année (notre CM2) que la calculatrice ( a calculator ) est introduite à l’école. Je pense que c’est tout à fait raisonnable. Voici un extrait du curriculum de Singapour :
« The learning of mathematics should focus on understanding, not just recall of facts or reproduction of procedures. Understanding is necessary for deep learning and mastery. Only with understanding can students be able to reason mathematically and apply mathematics to solve a range of problems. After all, problem solving is the focus of the mathematics curriculum. »
Understanding (la compréhension) martèle-t-on... Faire réussir sans comprendre n’est pas, assurément, la doctrine de l’école de Singapour ! À Singapour on a bien étudié toutes les techniques pédagogiques anciennes et modernes, y compris celles de l’Éducation Nouvelle. Mais ils ne sont pas restés figés à la pédagogie du début du 20e siècle. Ils en ont corrigé les faiblesses. « Sans hier et sans demain, aujourd’hui ne vaut rien. » disait Pierre-Jakès Hélias, mon excellent maître, à l’école normale d’instituteurs de Quimper. On l’a bien compris à Singapour. Et eux ils préparent leurs enfants aux défits technologiques du 21e siècle. Leur curriculum est bâti sur du roc. En France nos fondations reposent sur du sable. Et ce ne sont pas d’autres technocrates qui nous feront avancer. Que les instituteurs français correspondent directement avec leurs homologues Singapouriens ! Si le ministère de l’éducation nationale souhaite vraiment voir les enfants français faire de gros progrès, alors qu’il rende la pédagogie à ceux qui l’appliquent quotidiennement et leur fasse confiance. La conscience professionnelle est la première qualité de l’instituteur. Je ne suis pas devenu instituteur pour transformer mes élèves en simples consommateurs.
Il serait peut-être temps que les pédagogues français abandonnent l’idée qu’ils seraient les meilleurs du monde !
*
On n'enseigne pas de la même façon en math-sup, au lycée, au collège, et même au cours moyen, que dans une classe de cycle élémentaire.
* * * * *
Une étude de la DEPP (Rocher, 2008) a montré qu'après 1986, en une douzaine d'années, les performances en calcul des écoliers français se sont effondrées.
Au moment, où les derniers instituteurs, ayant eu une formation initiale, à l'école normale, avant les maths modernes, partent à la retraite. C'est un excellent exposé, passionnant, sur l'apprentissage des décompositions additives du nombre en maternelle. À chaque fois que je peux écouter Rémi Brissiaud, j'apprends quelque chose. J'ai revu cette émission plusieurs fois. Là, il convainc un convaincu. Et je le remercie vivement de réhabiliter le comptage dénombrement. En 1988, j'ai dû supprimer mon affichage mural de décompositions additives des nombres (dominos double cinq) qui était bien utile à mes élèves les plus faibles de CE2. Je ne manquerai pas de conseiller la lecture de Rémi Brissiaud à mon dernier "jeune" inspecteur, lorsque je le rencontrerai. Mais moi, j'ai visionné la vidéo, séquence par séquence, à tête reposée. Je plains les pauvres professeurs des écoles qui ont assisté à cette conférence. J'espère que les fauteuils étaient confortables. Trois heures à écouter un monologue sans le moindre échange entre l'orateur et la salle: drôle de modèle pédagogique ! Quel dommage que Rémi Brissiaud ignore les décompositions multiplicatives ! Lorsqu'on compare les mesures de la température sur un thermomètre, on pratique le calcul numérotage. Qui le sait ? Lorsque la température passe de 2° à 4°, fait-il deux fois plus chaud ? On peut faire des opérations additives et soustractives en lisant et en comparant les mesures d'un thermomètre. Et lorsqu'il fait très froid la température passe sous la barre de zéro degré. Alors, on peut lire des nombres négatifs. Mais on ne peut pas multiplier ni diviser les mesures de température en degrés. On voit bien l'importance des décompositions multiplicatives pour comprendre quand on fait du comptage dénombrement ou du comptage numérotage. Les marques tracées sur un thermomètre sont des bornes, des repères. C'est à partir d'eux qu'il est possible de faire différents calculs (nombres ordinaux ou cardinaux lorsqu'on a compris comment les combiner). Dans tout problème arithmétique, il est d'abord important de situer le repère du nombre du début de l'algorithme sur une échelle, de le comparer avec celui de la fin. Et on estime, puis on vérifie la justesse des calculs. Faire apprendre le comptage dénombrement en priorité est une condition nécessaire pour que la France revienne à son niveau de 1988. Ce n'est pas malheureusement une condition suffisante. Personne ne détient à lui seul toute la vérité pédagogique, pas même Rémi Brissiaud. Et moi, je ne connais pas de méthode miracle. Quand la France est lanterne rouge au classement TIMSS de CM1, que ce sont leurs propres livres, leurs propres méthodes, qui ont contribué à cette peu envieuse position, les chercheurs français devraient avoir l'humilité d'aller voir de près ce qui se passe à Singapour. Ne pas le faire, frise la faute professionnelle. Leur responsabilité est bien plus grande que celle des professeurs des écoles qui ne peuvent mettre en application que ce qu'ils savent et pas ce que les formateurs ne leur ont pas appris. Il est temps d'écarter les œillères. Les enfants de Singapour sont capables d'apprendre simultanément la multiplication et la division, grâce aux manipulations et aux schémas visuels. Pourquoi ne pourrait-on pas le faire en France ? Un quarteron de pédagogues français médiocres, ou imbus d'eux-mêmes, mais influents, ne l'admettront jamais. Ils feront tout pour pouvoir continuer à vendre leurs livres, leur matériel et leurs méthodes d'un autre âge mais qu'il prétendent modernes. La conférence de trois heures, ci-dessus, se termine par une opération de lobbying pour promouvoir une série de livres, du matériel que ne peuvent pas s'offrir les écoles les plus pauvres.
Le classement TIMSS 2015 ne reflète pas les capacités des petits français. C'est le résultat de la recherche pédagogique française. Les professeurs des écoles sont contraints d'appliquer ces méthodes douteuses, le petit doigt sur la couture du pantalon. Affirmer que le problème vient du profil non scientifique des enseignants du primaire, très majoritairement issus de filières littéraires ou de sciences humaines, est une façon peu élégante de se dédouaner de ses propres erreurs. Il y a quelques mois, je suis allé rendre une visite d'amitié à une Auxiliaire de Vie Scolaire en congé de maladie. Elle avait en charge une petite fille handicapée élève de CM1. Lorsqu'elle m'a montré la table de Pythagore de cette petite fille, j'ai pu constater qu'elle ne pourrait jamais retenir de façon pérenne ses tables de multiplication. J'ai passé toute l'après-midi avec cette amie, et à la fin, elle avait bien compris ma méthode. Malheureusement, lorsqu'elle a repris son travail elle n'a pas pu la mettre en œuvre. Il fallait que tout le monde pratique la même méthode dans la classe. C'était la méthode conseillée, donc imposée, par l'inspecteur. Je ne connaissais pas le rôle de l'AVS. Je pensais qu'elle suivait aussi l'élève en dehors des cours. Si cela avait été possible, mon amie aurait fait de cette enfant handicapée une tête de classe. Je précise que mon amie n'a aucun diplôme universitaire et était vendeuse dans un magasin de chaussures avant de perdre son emploi.
Je suis d'accord avec Rémi Brissiaud lorsqu'il affirme
« ... une méthode qui se dit de Singapour alors que, à l'opposé de ce qui se fait dans cette cité, elle enseigne le comptage-numérotage.» L'enseignement des tables de multiplication, ce n'est pas mieux, une traduction française de la méthode singapourienne qui plaît aux USA. Or ce grand pays est encore plus mal placé que la France au classement PISA et le restera tant qu'il demeurera dans sa tradition de droite numérotée. Le jour où Rémi Brissiaud aura admis que les enfants peuvent comprendre très tôt chaque sens de la division, les décompositions multiplicatives, et que sa religion pédagogique lui permettra d'accepter la potence de la division française dès l'apprentissage des tables de multiplication, alors, on pourra envisager de pouvoir rivaliser avec Singapour. La verbalisation de divisions de petits nombres, c'est tout de même plus astucieux et plus efficace que le drill et son antique et dangereux jeu du furet. C'est Rémi Brissiaud lui-même qui l'affirme : « L'un des principaux résultats en neurosciences cognitives, résultat qui a d'ailleurs valu un prix Nobel aux chercheurs l'ayant établi, est que la spatialisation joue un rôle crucial dans la mémorisation.» Merci donc aux chercheurs John O'Keefe, May-Britt et Edvard Moser. Ils ne font que conforter tout ce que j'ai pu écrire ici, notamment au sujet de la potence de la division. Si la technique opératoire de l'addition, de la soustraction et de la multiplication, peut être opposée à celle du calcul mental ou du calcul en ligne, il n'en est pas de même pour la division où on commence l'opération par la gauche et non par la droite. Il n'y a donc pas d'obstacle à tracer une potence dès l'apprentissage des tables de multiplication. Cette opération simple offre l'avantage de fournir aux enfants des repères spatiaux. Lors de la correction (multiplication ou division), l'élève au tableau, guidé par le maître, verbalise à haute voix. Les autres, à leur place, verbalisent intérieurement. Et en France, on verbalise en français, pas en américain. En attentant, on assiste à un triste maquignonnage dans l'édition du livre scolaire. Chacun voit la paille dans l'œil du voisin, mais pas la poutre dans le sien. C'est Médor qui défend son os ! Et cela fait marcher le commerce !
Lorsqu'on est un peu bricoleur, on peut remplacer tous ces produits par un matériel pédagogique tout aussi valable qui ne coûtera guère plus que l'huile de coude qui sert à le fabriquer. Et c'est bien cela qu'il faudrait enseigner dans les ESPE. Pour les tables de multiplication, le premier livre de CE2 de Singapour (excellent) n'impose que du papier quadrillé et une paire de ciseaux par élève. Pour la fiche de l'école libératrice, j'avais besoin de jetons. «Trop cher !» m'avait-on répondu à la mairie du village, en 1967. Somme dérisoire comparée au prix du matériel ci-dessus. J'avais remplacé les jetons par les boutons de la réserve de ma femme qui était couturière.  Construire un mètre pliant et quelques idées pour apprendre à l'utiliser... Construire un mètre pliant et quelques idées pour apprendre à l'utiliser...Ou comment représenter la file numérique des cardinaux suivant diverses lignes géométriques différentes. Rémi Brissiaud a-t-il lu vraiment le rapport Villani-Torossian ? N'y aurait-il pas un peu de mauvaise foi ?  Voir le texte intégral du rapport. Voir le texte intégral du rapport.
Moi, je lis : « Seule cette pratique permet d'échapper au risque souvent dénoncé par Rémi Brissiaud de réduire la notion de nombre à celle de comptage par récitation de la comptine numérique. Les jeux de groupements et de partages pratiqués dès l'école maternelle ouvrent la voie aux décompositions multiplicatives des nombres, en plus des décompositions additives.»  Voir l'article concerné Voir l'article concerné  Voir la mise au point de Cédric Villani Voir la mise au point de Cédric Villani Au mois de janvier 2018, le nouveau livre de CE2 de la librairie des écoles n'était pas encore en vente. Tous les membres de la commission avaient-ils vu cette version américanisée de la méthode de Singapour, avant de produire leur rapport ? Je viens seulement de découvrir le  BOEN. . BOEN. .Il aurait été si simple de se rendre sur le site de Singapour et de faire la traduction soi-même !
Il y a quelques années, j'étais intervenu sur le site de la Khan Academy. J'avais dit: "Les bons élèves ne font pas comme cela, mais 8+2+5=15." Et ils avaient réalisé une nouvelle vidéo: ( Dommage, que pour eux, ce ne soit pas une priorité et qu'ils n'aient pas abandonné le calcul-numérotage !)
Faire apprendre des suites numériques à des petits enfants, les parents et grands-parents l'ont toujours fait, même avant 1970, dans toutes les familles. Cela n'a jamais empêché un enfant d'aimer les maths. C'était au cours préparatoire qu'il ne fallait pas se tromper et privilégier le calcul-dénombrement.
Recommandations à Singapour avant d'entrer au CP
On apprend à dénombrer de 1 à 20 Lire et écrire ces petits nombres en chiffres et en lettres. On compare ces quantités. Plus ou moins (More or less). C’est différent de après ou avant : (Pas de droite numérique à Singapour). Enfin on apprend à situer des nombres dans la suite. (Spatialisation) À Singapour, on n'est pas monomaniaque ! Concernant les deux méthodes de techniques opératoires de la soustraction, où s'opposent Rémi Brissiaud et le ministre, pourrais-je les mettre d'accord ? Voici une troisième méthode qui concilie les deux premières.  La technique de la soustraction traditionnelle française apprise par cassage de le dizaine. La technique de la soustraction traditionnelle française apprise par cassage de le dizaine.
Concernant les tables de multiplication, je remarque le narcissisme de Rémi Brissiaud et je me demande s'il a ouvert le livre de CE2 de Singapour, celui préfacé par Laurent Lafforgue. Il faut être aveugle pour ne pas voir ce que les petits Singapouriens voient ! Le statut des tables n'est pas le même. Les enfants de Singapour ne se débrouillent pas trop mal en mathématiques. Où sont les utilisateurs de "J'apprends les maths" ? « Il n’est pire aveugle que celui qui ne veut pas voir. » À Singapour, les enfants apprennent des automatismes. Un algorithme comprend plusieurs étapes. La première a sans doute plus d'importance que la dernière. Les pauvres enfants qui subissent la méthode de Rémi Brissiaud ne peuvent apprendre que des réflexes. Et là, on comprend pourquoi les enfants français ne peuvent pas aimer les mathématiques. Ayant été, pendant des années, entraîneur de tennis de table, je peux expliquer la différence entre automatisme ou réflexe dans ce sport.  Voir: Automatisme ou réflexe en tennis de table Voir: Automatisme ou réflexe en tennis de tableVoici, sous la plume d'un rédacteur des revues France-TT et Bretagne-TT, un article qui me confère une certaine compétence technique dans ce domaine.  Voir cet article de presse. La gloire sportive est éphémère, surtout dans un sport invisible dans les médias. Voir cet article de presse. La gloire sportive est éphémère, surtout dans un sport invisible dans les médias.Il y a une analogie avec l'apprentissage des tables de multiplication. Moi, j'essaie d'éviter les mauvais réflexes. Rémi Brissiaud, avec son jeu du furet, il les provoque. Dans le jeu du furet, l’enfant émotif peut paniquer et donner une mauvaise réponse. Ce mauvais réflexe resurgira toute la vie durant. Les vieux instituteurs évitaient de commettre de telles erreurs. Dans son attaque à l'encontre du ministre, Rémi Brissiaud met en cause, gravement Roland Charnay. Je suis étonné que celui-ci n'ait pas réagi. Voici ce que préconise Roland Charnay.  Voir Voir Je me sens ici plus proche de Roland Charnay que de Rémi Brissiaud. Mais il n'y a aucune référence à la division. À Singapour, la division est le pendant de la multiplication. Et c'est bien par la recherche dichotomique dans les tables, les repères dans l'espace que les enfants peuvent mémoriser intelligemment les tables. On fait ces recherches pour apprendre la technique opératoire de la division, et c'est l'occupation des quatre places dans la potence qui aide l'enfant à comprendre les sens des problèmes de division. Dommage qu'on ne retrouve pas les principes énoncés ci-dessus dans Cap Maths où le calcul instrumenté prend une place trop importante et surtout trop précoce. Ce qui est dommageable pour les petits français, c'est que ces deux conceptions (Brissiaud - Charnay) sont antagonistes. Elles enferment nos petits écoliers dans des impasses en sens opposé. Et si ces pédagogues des mathématiques acceptaient de lever les yeux pour sortir des ornières qu'ils ont tracées; s'ils avaient l'humilité d'aller observer ce qui se fait le mieux dans le monde, à Singapour; peut-être, les petits français retrouveraient-ils la voie de la réussite? Mais que c'est difficile d'admettre ses erreurs ou son incompétence ! Rémi Brissiaud voyait du calcul-numérotage là où il n'y en avait pas, le BOEN du ministère. Sa tribune, c'est le Café Pédagogique. Pourquoi ne va-t-il pas expliquer au rédacteur en chef du Café qu'il est en train de faire la promotion du calcul-numérotage ?
Ces décompositions arbitraires n'apportent rien à la construction des nombres. Les enfants sont tributaires d'un outil: la droite numérique. En l'absence du support concret, les enfants sont contraints de mémoriser par cœur toutes les situations. C'est à dire de les retenir sans comprendre, utiliser des réflexes. Ce qui est grave, c'est qu'avec ce jeu informatique, on automatise le calcul numérotage. Voilà comment on fabrique des infirmes en calcul mental. Et c’est là que Rémi Brissiaud se fourvoie. Ce n’est pas la connaissance, par cœur, de la file numérique qui occasionne des troubles calculatoires, c’est son utilisation pour les calculs les plus simples. Il faut apprendre à combiner les nombres ordinaux et les nombres cardinaux. C’est ce que j’explique, au risque de me répéter, à ma page  « L'horloge et les nombres » , ma théorie élémentaire des nombres. « L'horloge et les nombres » , ma théorie élémentaire des nombres.
Si j'avais un conseil à donner à l'auteur de ce petit jeu, ce serait de matérialiser les gares des dizaines. Le calcul numérotage serait plus intelligent et pourrait être complémentaire du calcul dénombrement. La file numérique pourra avoir son importance, plus tard, pour les nombres plus grands, à condition d’y avoir des repères. Quant à moi, je pense que cette file numérique devra prendre diverses formes géométriques, suivant les situations. Elle pourra aussi prendre la forme circulaire d’un cadran d’horloge avec diverses suites de nombres. On pourra même y situer des nombres fractionnaires. Rémi Brissiaud est un incompris: Déjà en 2016 :  TIMSS : Rémi Brissiaud : Erreur de diagnostic au Cnesco TIMSS : Rémi Brissiaud : Erreur de diagnostic au Cnesco
Mais il y a une bonne raison à cette incompréhension. J'espère qu'il la trouvera lui-même. Je ne voudrais pas être trop désobligeant. Ah! Je vous mets sur la voie. Un article de presse titrait:  Formation continue : plus de sept professeurs des écoles sur dix n'en retirent « rien » Formation continue : plus de sept professeurs des écoles sur dix n'en retirent « rien »
Quand les formations ressemblent aux sermons du prêtre, quand on n'accepte pas la contradiction... Lisez la dernière contribution de Rémi Brissiaud expliquant le si-problème et le cc-problème. On peut avoir de bonnes idées, mais voilà comment on fait fuir ceux qui ne sont pas pré-disposés à suivre une telle formation. Des 30% restants, il faut encore faire la distinction entre les gens sérieux et les moutons de Panurge. Nous ne sommes pas près de retrouver notre niveau de 1988 ! J'ai donc quelques divergences avec Rémi Brissiaud, mais force est de constater qu'il continue à chercher avec pugnacité et peut-être à trouver comment rattraper ce retard. Les noums : c'est une application informatique où Rémi Brissiaud utilise un concept qui m'est cher.  http://www.rriou.infini.fr/nouveautes/ http://www.rriou.infini.fr/nouveautes/
Claire Lommé expose avec beaucoup d'enthousiasme les principaux atouts de cette méthode.  http://www.cafepedagogique.net/lexpresso/Pages/2019/12/04122019Article637110405914998753.aspx http://www.cafepedagogique.net/lexpresso/Pages/2019/12/04122019Article637110405914998753.aspxJ'ajouterai que ce concept permet de tirer tout le monde vers le haut, de ne laisser personne à la traîne. C'est la construction d'images mentales à la portée de tous. Quand, en France, arrêtera-t-on de vanter la recherche pédagogique américaine. On y fait beaucoup d'expérimentations, mais les progrès ne sont pas là. Les USA occupent la 37e place au dernier classement Pisa, en mathématiques, avec 478 pts, loin derrière la France qui n'est pourtant pas brillante (25e, 495 pts) et surtout des premiers (555 pts). Les USA précèdent la France en compréhension de l'écrit et en sciences. Cette droite numérique américaine ne permet que des calculs sur les numéros, des apprentissages par cœur, des réflexes. Il n'y a pas d'automatisme possible, aucune image mentale ! Si Rémi Brissiaud et Stanislas Dehaène réfléchissaient au remplacement de la droite numérique par mon mètre pliant à dix brins, ne pourraient-ils pas rapprocher leurs points de vue et enfin s'unir pour définir un enseignement des nombres efficace, et peut-être, faire mieux que Singapour ? J’ai beaucoup de sympathie et d’estime pour ces deux personnalités qui comptent beaucoup dans le paysage de la pédagogie française des mathématiques. Tant qu’il y aura une opposition stérile d’idées, il n’y aura pas de progrès possible. Dans les années 70-80, nos pédagogues français, fascinés, d'abord, par les mathématiques modernes, sont allés, ensuite, chercher des idées outre Atlantique, pour les enseigner dans nos école normales. Ils ont américanisé le calcul. Les professeurs qui nous avaient (bien) préparés au baccalauréat en classes de seconde, première et terminale, durent se recycler. On ferma aussi les classes de troisième spéciale dans les collèges. Ce fut le moment où les politiques cassèrent l'ascenseur social. J'ai suivi un stage de Français, à l'école normale, sur recommandation syndicale. Il leur fallait des élèves. Et maintenant, à ces nouveaux formateurs, la pédagogie, et aux instituteurs ce qu'ils appelaient, dédaigneusement, des recettes... J'ai été formé aux mathématiques modernes, sur la base du volontariat et du bénévolat, le soir, après la classe, par les professeurs du collège (deux PEGC), au chef lieu de canton. Après les cours, on continuait à discuter mathématiques, devant une consommation, au café du coin. C'est la meilleure formation que j'ai reçue, tout au long de ma carrière. Pour mes élèves, il est heureux que je n'ai pas suivi le recyclage des mathématiques modernes par les nouveaux pédagogues. À l'examen d'entrée en 6e, autrefois, l'épreuve de calcul comprenait un problème noté sur 12 et quatre opérations notées sur 8 (avec souvent la preuve par 9 exigée). Lorsqu'on a supprimé l'examen, il fut remplacé par un dossier (Chemise rose pour les filles, bleue pour les garçons). Il comprenait outre le dossier et le livret scolaires, le cahier de compositions (CM1-CM2), renommé cahier de travail mensuel, mais sans classement. Chaque mois, malgré les mathématiques modernes, on a continué à faire des problèmes de révision et ces fameuses opérations avec la preuve par 9. Cela a continué jusqu'en 1992. Les nouveaux pédagogues et les historiens de l'éducation qui regardent l'école par le bout de la lorgnette qui les arrange, grossissant les défauts de l'école d'autrefois, mais ignorant, ou même masquant et dénigrant ce qui fonctionnait bien, se sont-ils aperçus qu'il fallait apprendre les tables de multiplication pour pouvoir réussir les opérations et raisonner concrètement pour trouver la solution des problèmes ? De nombreuses leçons ne figuraient pas dans mon journal de classe, ni dans celui des élèves, l'alibi pour la hiérarchie. Ceux qui critiquent les instituteurs d'autrefois, uniquement sur l'étude des cahiers d'élèves, ne peuvent être que dans la caricature. Au cours de ma carrière, j'ai été inspecté une dizaine de fois. Absolument personne n'a ouvert un cahier de brouillon d'élèves. Or c'est là qu'on pouvait suivre leurs essais, leurs erreurs, leurs vérifications.... Tout ce travail, l'inspecteur ne le voyait pas. Ce savoir-faire n'a pas été transmis aux nouvelles générations de professeurs des écoles. Par exemple, moi, j'utilisais deux livres; Postel (mathématique moderne) plus Vassort; puis ensuite, Eiler, pour faire plaisir à mon inspecteur, avec Vassort que je réactualisais, car les livres des élèves étaient en piteux état, à force d'être manipulés au fil des ans, et aussi, bien sûr, mes fiches de l'école libératrice, pour la réussite de mes élèves. Et il ne fallait pas compter sur moi pour faire la division par soustractions successives du livre Eiller !!! Méthode ridicule en terme de rapidité calculatoire et pire, qui ignorait la dichotomie, faisant perdre les repères des tables de multiplication. Les tables de multiplication avaient donc disparu des nouveaux livres. Seule la table de Pythagore avait droit de cité. Heureusement, les enfants et les parents trouvaient les tables traditionnelles, au dos des cahiers de brouillon.
« Sans hier et sans demain, aujourd'hui ne vaut rien. »
Il suffit d'aller voir comment on procède, aux USA, pour comprendre l'effondrement des résultats en calcul de nos petits Français.
On trouve un autre exemple de l'américanisation du calcul dans la presse sportive: Les journalistes français s'alignent sur le modèle anglo-saxon. Les relais 4 x 400 m. Avant 1970, pour trouver la distance parcourue par chaque équipe, on aurait écrit: Distance totale parcourue: 400 m x 4 = 1600 m En mathématiques modernes, on aurait écrit: Distance totale (400 x 4) 400 x 4 = 1600 Chaque équipe va parcourir 1 600 mètres. À Singapour, tout le monde parle le même langage. Maintenant, après l'épisode interminable des maths modernes, en France, c'est l'anarchie. Avant 1970 : Multiplicande (nombre concret) multiplié par le multiplicateur (nombre abstrait) égale le produit (nombre concret). Maths modernes: (a multiplié par b) égale (b multiplié par a) (tous les nombres sont abstraits) Puis maintenant on parle de remettre des unités de grandeur dans les opérations. Et chacun fait ce qu'il veut. Comment voulez-vous qu'un enfant s'y retrouve ? La première difficulté à surmonter en technique opératoire, c'est la représentation spatiale. Chaque chose doit être à sa place ! Moi, qui ai adoré les maths modernes, je raisonne en termes d'opérateurs, car c'est grâce à eux qu'on peut introduire la programmation informatique (données numériques et alpha-numériques). Mais de grâce, messieurs les mathématiciens et autres professeurs de mathématiques, mettez-vous d'accord une fois pour toutes et laissez les professeurs des écoles travailler sereinement. Chacun son métier !
Le grand mathématicien russe, Vladimir Arnold, aimait à se moquer de l'enseignement des mathématiques modernes en France:
« Lorsqu'on demande à un petit Français : "Que vaut 2 + 3 ?"
Il dit: "2+3 = 3+2 parce que l'addition est commutative."
« Le calcul doit se référer à des situations concrètes, indispensables compléments et supports du développement des capacités abstraites.»
Voici une avancée essentielle publiée dans
«L'usage des mots précède celui des symboles mathématiques. L'introduction et l'utilisation de ces derniers sont réalisées au fur et à mesure qu'ils prennent sens dans des situations d'action et en relation avec le vocabulaire.»
Mais dès la mise à jour du 15 avril : 6 x 7 = 7+7+7+7+7+7 (Comme aux USA: 6 groupes de 7.) En Breton, onze (11) se dit un-dix; dix-sept (17), sept-dix; mais dix-huit (18), 3 fois 6. Quarante (40), c'est 2 fois 20; soixante (60), c'est 3 fois 20; quatre-vingts (80), c'est 4 fois 20; cinquante (50), c'est la moitié de cent. Si les chinois sont avantagés en numération (base 10), les bretons ont un avantage tout aussi évident (décompositions multiplicatives) pour la compréhension de la division. Le plus difficile, c'est de passer d'une langue à l'autre. Je suis donc bien placé pour mesurer les difficultés d'apprendre les automatismes de calcul dans une langue différente de sa langue maternelle. Une ancienne élève, d'origine portugaise, m'a fait la remarque, qu'elle aussi, avait eu du mal en calcul mental oral, alors qu'elle était très à l'aise en calcul rapide écrit. D'où l'importance d'avoir pour références mentales, des croquis, des schémas visuels résumant des manipulations. Il y a quatre langues parlées à Singapour, l'anglais, le mandarin, le malais, le tamoul. À l'école, les cours se font en anglais. Les pédagogues de Singapour ont des années-lumière d'avance sur les "experts" français d'aujourd'hui. Eux, ils préparent l'avenir de leurs enfants aux compétitions du 21e siècle. Il est possible que les méthodes françaises fonctionnent bien dans les écoles de centre ville où les parents aisés intellectuellement peuvent aider leurs enfants en compensant les grossières erreurs des pédagogues français. Mais tous les autres, ne peuvent mémoriser qu'à l'aide de l'ouïe (J'entends et j'oublie...). C'est difficile quand on n'a pas de repères linguistiques.
 (voir plus bas: le problème du train de Narbonne, erreur de repères); où le vocabulaire est imprécis, flou; où l'on apprend à répondre mécaniquement (usage de la commutativité sans comprendre le problème); j'aurais été nul en mathématiques. (voir plus bas: le problème du train de Narbonne, erreur de repères); où le vocabulaire est imprécis, flou; où l'on apprend à répondre mécaniquement (usage de la commutativité sans comprendre le problème); j'aurais été nul en mathématiques."Le français ne fait jamais ses comptes comme le breton. Allez donc vous y retrouver." disait mon excellent maître Pierre-Jakes HELIAS. J'étais entré au CP avec un an d'avance. Tout cela, parce que l'instituteur avait épousé la fille de l'épicière du village, là où ma mère m'envoyait faire les petites commissions. Je passais pour un petit phénomène. Ma mère m'avait appris à lire l'heure, en breton, vers quatre ans sur une horloge aux nombres romains  Voir et à compter en utilisant les pièces de monnaie. Voir et à compter en utilisant les pièces de monnaie.C'est simple, quand on utilise la numération bretonne à base 20 (On utilise aussi les doigts de pieds pour compter. 10, c'est la moitié de 20, 5 le quart de 20 et moitié de 10.). Les pièces des dizaines (20F, 10F et 50F) étaient jaunes. Les pièces des unités (1F, 2F et 5F) étaient blanches, en aluminium. Combien de pièces de 20F pour faire 40F, 60F, 80F, 100F ? C'est la division quotition. 50, moitié de 100. C'est la division partition. Bien avant l'âge d'entrer au CP, je maîtrisais parfaitement chaque sens des quatre opérations parce que ma langue maternelle, dans laquelle je réfléchissais, je parlais, c'était le breton. Si le nombre 18 avait causé du souci à Pierre-Jakez Hélias, pour moi, 3 fois 6, c'était la suite logique sur le cadran de l'horloge (6,12,18). 12 valant midi et minuit. Ensuite, mon jouet offert par mon oncle Joseph, le mètre pliant métallique à 10 brins du maçon, m'a permis de bien assimiler la numération décimale (base 10) .  Construire un mètre pliant et quelques idées pour apprendre à l'utiliser... Construire un mètre pliant et quelques idées pour apprendre à l'utiliser...
Pour vous aider à bien comprendre les comptes de Pierre-Jakes Hélias
Qui a osé affirmer qu'un enfant de CP ne peut pas comprendre les notions de multiplications et de divisions ? Il faut être née avec une cuillère d'argent dans la bouche ou une idéologue qui n’a jamais enseigné dans une classe d’école primaire, pour prétendre que l'utilisation des pièces de monnaie nuit à la compréhension du nombre. Mes parents élevaient une vache. Comme nous n'avions pas assez de terres, j'accompagnais ma mère le long des chemins, afin que notre vache broute l'herbe des fossés. Lorsque je portais le bidon de lait à l'épicière, je savais parfaitement ce que cela représentait. Je savais quelle somme il me resterait après avoir fait mes petites commissions. Mais je n'étais pas un enfant surdoué. Ma mère, qui avait quitté l'école à dix ans, était meilleure pédagogue que les auteurs des livres de mathématiques utilisés, aujourd'hui, par les petits français ou que ces idéologues qui ont copieusement bien vendu leurs livres et leurré, dupé les jeunes professeurs des écoles et la population en général. Fort de mon expérience personnelle, je me demande si les chercheurs français n'en demandent pas un peu trop aux enfants de maternelle, et si les querelles techniques Brissiaud vs Dehaène ne sont pas un peu vaines:
En chinois, la langue parlée suit exactement le système décimal de position des chiffres. Les chercheurs qui se sont intéressés à cette question ont montré que les enfants de Chine apprennent plus vite les nombres que les enfants de France, mais ces derniers rattrapent leur retard et n'ont finalement pas plus de difficulté à comprendre et utiliser les nombres.
Le moment le plus important ne serait-il pas vers 7 - 8 ans, à l'âge de raison, lorsque l'enfant devient capable d'inhiber les mauvais automatismes, comme l'affirme Olivier Houdé ?
Enseigner les mathématiques - Belin (page 253)
C'est aussi le moment de l'apprentissage des tables de multiplication. À Singapour, les enfants ne sont pas aussi en avance qu'on le voudrait en France, à l'entrée au CP... Et pourtant, constatons les résultats à TIMMS et à PISA. Privilégier la précision du vocabulaire et apprendre à se repérer dans l'espace et dans le temps, cela me semblerait plus judicieux. Ce n'est évidemment qu'une opinion personnelle. Il ne faut pas confondre tables de multiplications et tables des multiples, l'oral et l'écrit. Pendant la période de découverte les deux formes de tables doivent être vues (comme à Singapour), et simultanément, ligne par ligne, méthodiquement, car cela aide à la compréhension et permettra de retenir intelligemment les tables. On mémorise d'abord des schémas, des algorithmes. Comprendre un algorithme, c'est savoir le décomposer, puis le reconstituer, étape par étape, dans l'ordre. Mais pour l'apprentissage par cœur, il est impératif de privilégier les tables de multiplications avec le mot fois, le son fois. À l'oral on ne réfléchit pas comme à l'écrit. On répond plus vite. Or, on sait déjà que 3 fois 2 et 2 fois 3 donnent le même résultat.
Décompositions multiplicatives Les décompositions additives de 4 sont : (0 et 4), (1 et 3), (2 et 2), (3 et 1) et (4 et 0) Les décompositions multiplicatives de 4 sont : (1 fois 4), (2 fois 2) et (4 fois 1) Les décompositions multiplicatives de 6 sont : (1 fois 6), (2 fois 3), (3 fois 2) et (6 fois 1). On peut en retrouver quelques unes, concrètement, en alignant 6 éléments sur une table, et en dessinant des ensembles.
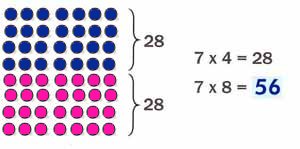
Par exemple, 7 fois 8 c'est 1 fois 8 plus 6 fois 8 2 fois 8 plus 5 fois 8 3 fois 8 plus 4 fois 8 4 fois 8 plus 3 fois 8 5 fois 8 plus 2 fois 8 6 fois 8 plus 1 fois 8 Mais 8 fois 7 , c'est 1 fois 7 plus 7 fois 7 2 fois 7 plus 6 fois 7 3 fois 7 plus 5 fois 7 4 fois 7 plus 4 fois 7 5 fois 7 plus 3 fois 7 6 fois 7 plus 2 fois 7 7 fois 7 plus 1 fois 7 Les tables x5 et x2 sont les plus faciles à mémoriser et, à l'entrée au CE2, les enfants devraient les connaître, déjà, parfaitement. On va donc pouvoir insister sur les schémas de 5 fois 8 plus 2 fois 8, soit 40+16=56 ou , après avoir déplacé la table des enfants, sous un autre angle, 5 fois 7 plus 3 fois 7, soit 35+21=56 À Singapour on retient 4 fois 7 plus 4 fois 7, c'est à dire 28+28=56 ou 2 fois 28 font 56. En calcul mental, c'est aussi 40 + 16 (2 fois 20 plus 2 fois 8) Il y a d'autres décompositions possibles. Faites confiance aux enfants pour les trouver ! C'est le moment idéal pour mettre en valeur l'intelligence des plus faibles. C'est par ces manipulations qu'ils prennent confiance en eux et ils vont apprendre à ne pas détester les maths. Mais le rôle de l'instituteur consistera aussi à apprendre à l'enfant à écarter les algorithmes trop compliqués pour ne conserver que les plus judicieux. Peut-être, même, certains parviendront-ils à mémoriser, par le même algorithme, toute la table x7. Le schéma ci-dessous m'a été inspiré par le matériel Picbille. Mais le livre du maître de "J'apprends les maths" n'appelle pas à faire les manipulations adéquates. On y préfère le "drill" et le catastrophique jeu, soi-disant moderne, du furet, par opposition au concurrent "Cap maths" qui fait apprendre par cœur la table de Pythagore. Mais, monsieur Brissiaud, il y a d'autres manières de mémoriser ! Comme à Singapour, par exemple ! 
Table de multiplication
Ce n'est que lorsque l'un des schémas aura été mémorisé mentalement et le résultat obtenu avec sûreté, qu'on pourra compléter par un moyen mnémotechnique. Pour 7 fois 8 ou 8 fois 7, les bretons sont favorisés: 56, c'est le Morbihan. Ensuite, la récitation de chaque ligne des tables doit devenir automatique. Il faut donc, alors, s'appuyer sur l'oral et apprendre les tables en utilisant celles que je présente ci-dessous et qui sont, à mon avis, les mieux adaptées à la mémorisation verbale. Les mauvaises habitudes, prises par l'apprentissage oral des tables des multiples, avec le signe x plutôt que le son fois, peuvent devenir un handicap, surtout pour les élèves qui n'ont pas les capacités logiques adéquates. C'est prendre l'omnibus au lieu du TGV. Les bons ouvrages sont rares. Je recommande celui-ci : aux éditions Buissonnières à CROZON (29) On ne peut pas provoquer la bonne réponse réflexe, chez l'enfant, sur simple commande, mais on doit, surtout, lui éviter de prononcer des erreurs dès les premiers essais, éviter de fabriquer un mauvais réflexe. C'est ce que propose admirablement cet ouvrage. Ecoutez aussi, ce que préconise Rémi Brissiaud (Seulement, le dernier fichier. Je ne suis pas toujours en accord avec ce qu'il dit par ailleurs. Mais personne ne détient à lui seul, toute la vérité. Ni lui, ni moi.) Pour l'apprentissage par cœur, je préfère la méthode de Jean-Pierre Lefort, (éditions Buissonnières) à celle de Rémi Brissaud. Je pense que le jeu du furet, avec association verbale, à ce stade de l'apprentissage des tables, est risqué. On ne maîtrise pas les réponses des élèves. Une première réponse erronée peut provoquer un mauvais réflexe, comme celui de Didier Migaud. En tout début de l'apprentissage des tables, il faut laisser du temps à l'enfant pour lui permettre de réfléchir. Sinon, il va stresser, paniquer et donner une réponse fausse qui lui restera toute sa vie et qu'il aura du mal à inhiber. Concernant l'apprentissage des tables de multiplication, j'ai quelques points de convergences avec ce qu'écrit Rémi Brissiaud dans le livre du maître de CE2. «L'usage des tables traditionnelles conduit à apprendre les expressions à mémoriser au sein d'une même table, dans l'ordre. Or, on sait, depuis les travaux des philosophes grecs, que l'ordre est une mnémotechnique. De plus, l'usage «moderne» de ces tables, qui vient d'être décrit, permet d'éviter tout phénomène de dépendance à cette récitation dans l'ordre.» Mais le jeu du furet vient trop tôt, sa méthode manque de véritables manipulations (commutativité admise d'emblée sans être démontrée) et surtout, il néglige l'apport de la division euclidienne, les bornes d'intervalles. Avec ce jeu du furet, présenté comme moderne, Rémi Brissiaud commet une faute pédagogique monumentale. Au début, on ne récite pas une table, on la lit ! On évite de créer un mauvais réflexe. Dans ma méthode, celle de "L'école libératrice", les enfants ne construisent pas seuls les tables. Les mêmes schémas servent pour la multiplication et la division. Je les mène rigoureusement là où j'ai décidé de les envoyer. Les gestes de base sont construits sans faute. Les interférences pénalisantes qu'on retrouve souvent dans les méthodes de reconstruction critiquées par Rémi Brissiaud, sont, ici, très limitées. Les enfants ont le choix parmi plusieurs algorithmes pour retrouver le résultat, et non un seul. Mais le maître est là pour leur suggérer le meilleur. La lubie des enfants qui construisent seuls leur savoir, au petit bonheur la chance, ne peut pas s'appliquer, surtout, à l'apprentissage des tables de multiplication. C'est aussi vers la fin des années 80, qu'est née l'idée développée par les "pédagogues" et certains inspecteurs, d'opposer mémoire et intelligence. Tout travail répétitif serait du dressage. Alors ne nous étonnons plus, que lorsqu'un ministre a remis les tables de multiplication à l'honneur, plus personne ne sache vraiment apprendre aux enfants à mémoriser intelligemment et que certains confondent réflexes et automatismes. Cela faisait quarante ans que les tables traditionnelles avaient disparu des livres recommandés voire imposés par les inspecteurs. C'est tellement énorme que cela frise le ridicule. Il est aberrant que seuls les chercheurs professionnels aient le pouvoir de faire de la recherche pédagogique. Ils ne sont pas d'accord entre eux. Et si l'on veut dire du mal de l'un, il suffit de lire ce qu'écrivent les autres. Les principaux outils pédagogiques efficaces ont été inventés par des instituteurs (Célestin Freinet, Georges Cuisenaire....). C' est l'occasion qui fait le larron. L'instituteur consciencieux est perpétuellement en situation de rechercher la technique qui lui permettra de faire passer un savoir. Et chaque élève est unique car chacun a son propre passé. Ce qui marche avec l'un ne fonctionnera peut-être pas avec l'autre. Aujourd'hui, pour la mémorisation verbale, je ferais créer des fichiers mp3 par les élèves :  Voir le mode d'emploi Voir le mode d'emploiJe ne peux pas vérifier l'efficacité de cette méthode. Si un jeune collègue l'essaie, je le remercie à l'avance, de me tenir au courant de ses observations. Avant de m'exprimer sur l'apprentissages des tables de multiplication, je pense nécessaire d'expliquer la différence entre un automatisme et un réflexe. Je peux l'expliquer très simplement d'après ma longue expérience d'entraîneur de tennis de table. Si un chercheur passe par ici, j'aimerais qu'il puisse m'expliquer la différence entre les deux sortes de réflexes que j'ai pu observer : réflexe (panique) et réflexe (automatisme robotisé).  Voir: Automatisme ou réflexe en tennis de table Voir: Automatisme ou réflexe en tennis de table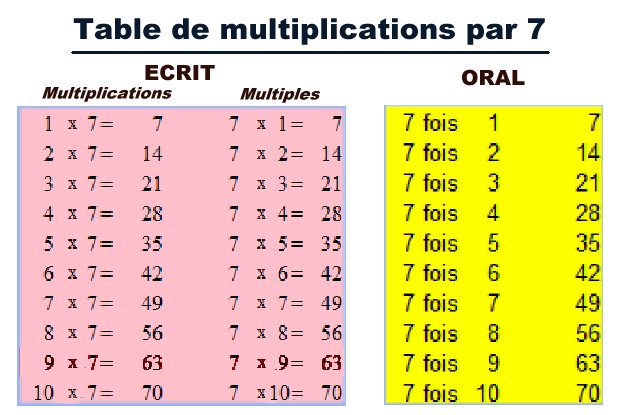
Autrefois, on trouvait les tables à apprendre par cœur, avec le mot fois, au dos des cahiers de brouillon ou des protège-cahiers. On ne prononçait pas égal. Tous les parents pouvaient être des répétiteurs efficaces. Le sommeil joue un rôle important dans la mémorisation.
J'en avais la conviction depuis ma formation initiale en 1962, cours de monsieur Joseph Le Poezat-Guigner, un expert ex-pair (instituteur, inspecteur puis directeur d'école normale). Croyance renforcée par un cours de professeur d'université à l'occasion d'un stage d'entraîneur sportif, de haut niveau, en 1971, à l'INS (maintenant INSEP). Ce n'est pas au parent de faire la leçon, mais une petite piqûre de rappel juste avant le coucher va sensibiliser l'enfant qui va se remémorer les manipulations, les schémas et les algorithmes étudiés dans la journée. Maintenant, c'est une certitude !
Il faudra attendre les travaux de Karni et coll. (1994), puis ceux des équipes de Stickgold, Ribeiro, et Born, pour prouver que, sans aucun entraînement supplémentaire, les performances cognitives et motrices s'améliorent significativement et de façon durable après une période de sommeil, alors la perturbation du sommeil bloque sélectivement cette consolidation.
(Stanislas Dehaene)
Et surtout, que les enfants aillent au lit de bonne heure ! Aujourd'hui, on ne trouve ces tables, nulle part. Les livres de cours élémentaire, majoritairement, présentent les tables des multiples avec le signe x (multiplié par) et avec le signe =. Il me semble que les éditeurs de livres scolaires devraient se pencher sur ce problème. La table la plus difficile à mémoriser, celle qu'on apprend en dernier, c'est la table par 7. Certains journalistes malicieux s'amusent à piéger les hommes politiques. La question combien font 7 fois 9 posée au président de la cour des comptes n'était pas anodine. http://www.rue89.com/2010/10/07/didier-migaud-ne-connait-pas-ses-tables-de-multiplication-169973 Pourquoi aucun pédagogue n'est venu défendre Didier Migaud ? Ce type d'erreurs est bien connu. Il s'agit d'une réponse réflexe (un mauvais réflexe), à ne pas confondre avec un automatisme. Tous les vieux instituteurs ont pu constater des erreurs de ce type au cours de leur carrière. Et la différence entre réflexes et automatismes est bien connue dans les sports où les réflexes ont un rôle majeur, tennis de table, par exemple.
Vers 1970, j'avais fait apprendre la récitation « Le laboureur et ses enfants » dans ma classe. Je n'avais pas vu qu'un élève avait écrit sur son cahier « gardes-vous leur dit-il » au lieu de « gardez-vous leur dit-il » et il commit l'erreur à la première récitation. Bien sûr on corrigea la faute à l'écrit, à l'oral, et apparemment, c'était compris et retenu. Mais le jour de la fête de Noël, il récita son texte en public, assez ému; et je me souviens encore du mouvement de menton de mon Père Noël, un poilu de la guerre 1914-1918, lorsque nous entendîmes « Gardes-à-vous !».
Je n'ai aucun souci pour Didier Migaud, car depuis 50 ans il n'a plus eu à utiliser les tables à l'oral dans un contexte scolaire, mais à l'écrit, où la personne ayant un esprit cartésien se réfère plutôt à des algorithmes qu'à la mémoire dite visuelle ou auditive. Ce doit être plus problématique pour des personnes qui n'ont pas les qualités logiques adéquates et qui n'ont pas eu les bons réflexes au départ. Je suppose que Didier Migaud avait prononcé sept fois neuf : soixante-seize la première fois, mais que son instituteur avait fait corriger puis répéter ensuite la ligne correcte, qui était devenue un automatisme. Réfléchissant à une autre question du journaliste, c'est la réponse réflexe qui est sortie de sa bouche. Il y avait trop longtemps qu'il n'avait pas entraîné ses automatismes. Cela m'étonnerait que Didier Migaud aurait fait la même erreur si on lui avait posé la question par écrit. Le même journaliste essaie de prendre en défaut Olivier Besancenot (9 fois 8) http://www.rmc.fr/editorial/145988/olivier-besancenot-ne-connait-pas-ses-tables-de-multiplication/ qui préfère renoncer à répondre: et il a bien raison. Jean-Jacques Bourdin parviendrait à piéger un médaillé Fields. Les réactions des internautes sont stupides. Ça n'a pas marché avec Cédric Villani, le 5 septembre 2019.  https://rmc.bfmtv.com/mediaplayer/video/le-mathematicien-cedric-villani-connait-il-bien-ses-tables-de-multiplications-1184515.html https://rmc.bfmtv.com/mediaplayer/video/le-mathematicien-cedric-villani-connait-il-bien-ses-tables-de-multiplications-1184515.html
Notre médaillé Fields prend une seconde de réflexion avant de répondre. Avec les calculatrices et les nouvelles technologies on oublie qu'en mathématiques, il faut d'abord manipuler, dessiner, visualiser, raisonner et faire des efforts. Pour apprendre, il faut se représenter mentalement ce qu'on découvre. . Pourtant, l'imagerie cérébrale peut aider à comprendre ces phénomènes. Stanislas Dehaene ou Olivier Houdé, par exemples ont écrit des choses intéressantes. Le vocabulaire utilisé est à la portée de tous. J'aimerais voir les pédagogues commenter leurs observations et déductions. Il faudrait éviter les interprétations abusives. De l'acte réflexe, j'ai retenu que l'influx nerveux part de la moelle épinière et non du cerveau. La première fois, c'est dans un terrain vierge que l'influx nerveux se creuse un chemin pour exécuter cet acte. Puis, le cerveau va mémoriser ce chemin. Ensuite, à chaque fois que l'on va exécuter ce réflexe, c'est le même chemin qui sera suivi. (Exposé de l'INS) Où ces chemins seraient-ils stockés dans notre cerveau ? Voici une réponse :
Il arrive qu'à la suite d'un A.V.C., à l'âge adulte, des personnes perdent brutalement toute capacité de calculer. Tel était le cas de MM, qui a brutalement perdu la capacité de résoudre des opérations aussi simples que « trois moins un ». De façon surprenante, MM parvenait encore à réciter les tables de multiplications.
... Cette région, le gyrus angulaire, interviendrait dans la mémorisation des « tables » de multiplication, réalisée essentiellement par récitation automatique de séquences apprises par cœur (« trois fois neuf égale vingt-sept »). Paragraphes extraits de La dyscalculie développementale,un trouble primaire de la perception des nombres de Nicolas Molko, Anna Wilson, Stanislas Dehaene Je dois avouer que je serais incapable d'expliquer ce qu'est la dyscalculie développementale. Je n'ai jamais suivi de formation de psychologie cognitive. La déduction que je fais de l'expérience, n'est pas celle des auteurs de l'article scientifique. Mais l'ancien instituteur que je suis, a maintenant une meilleure compréhension du réflexe différent d'un automatisme, une certitude. Mes mots n'appartiennent pas toujours au vocabulaire de cette recherche scientifique. Je prie les lecteurs de bien vouloir m'excuser. Je ne souhaite aucun désagrément à Didier Migaud, mais si un tel malheur lui arrivait, je laisse au lecteur de cette page imaginer quelle serait sa réponse à 9 fois 7. ou 7 fois 9. A la page 152 de son livre « La bosse des maths », Stanislas Dehaene se pose la question de savoir si la calculatrice doit se substituer à l'apprentissage du calcul mental, puis il cite un exemple d'éducation bien conçue, la Chine. Je suis étonné que ce savant qui aurait pu être mon élève ait appris toutes ses tables en chantant. Je l'avais fait aussi une vingtaine d'années plus tôt que lui. Cela ne l'a pas empêché de devenir un grand savant, ni moi de devenir un modeste instituteur. Cela permettait aux enfants bègues de mémoriser les tables. Avant 1970, l'Ecole Libératrice, revue du SNI (Syndicat national des instituteurs), publiait chaque semaine tout un fascicule de modèles de fiches pratiques. C'est là, que j'ai découvert cette méthode géniale que j'ai utilisée, avec bonheur, du premier au dernier jour. Elle n'a pas grand chose à envier à la pratique chinoise. Ce sont les schémas qui ont vocation à être mémorisés. Ce sont les mêmes que ceux enseignés à Singapour. Des tables des protège-cahiers, je n'ai conservé que les multiplications (elles servent aussi pour les divisions). L'apprentissage des tables ne se limite pas à les mémoriser verbalement. Ce n'est que la fin d'un processus s'étalant dans le temps, mais intervenant autrefois au CE2. C'est la disposition géométrique d'objets, leur manipulation, leur observation, leur représentation, qui va donner du sens à chaque opération (multiplication ou division). Les tables d'additions sont mémorisées facilement car le plus grand nombre est 18. En fait, le bon élève ne retient, d'abord, par la mécanique verbale du réflexe, qu'un nombre limité de lignes. Ne confondons pas calcul écrit rapide et calcul opératoire mental oral. Ainsi, la somme 9 + 8 =17 peut être retenue en utilisant les compléments à 10 ou la table des doubles. ( Et oui, monsieur Brissiaud, un breton n'oublie pas les décompositions multiplicatives !) (9 + 1 +7) (8 + 2 +7) ((2 fois 8 ou 8+8 )+1 ) ((2 fois 9 ou 9+9)-1) Rémi Brissiaud fait remarquer que le temps de réaction est plus long pour répondre à une addition qu'à une multiplication. Un automatisme raisonné (cerveau) est en effet plus lent qu'un réflexe (moelle épinière). Mémoriser les petits nombres des débuts des tables de multiplications, ne présente pas de grosses difficultés, grâce à des décompositions additives. On mémorise les grands nombres des tables par décompositions multiplicatives. Et en présentant simultanément tables de multiplications et tables des multiples, on limite les lignes de tables à retenir mécaniquement par la mémoire verbale. N'est-ce pas ce que souhaite Stanislas Dehaene ? Mais les lignes de tables correctement comprises et apprises puis, enfin, mémorisées verbalement, vont permetttre aux enfants de réagir plus rapidement, sans hésiter, sans erreur, en calcul mental et face à des problèmes plus compliqués. Les enfants ne raisonnent pas tous à la même vitesse. Le passage du concret à l'abstrait peut être laborieux. Certains ont besoin d'un support visuel pour les aider à mémoriser. Je recommande de tapisser les murs de la classe d'images comme celles-ci :
Voici ce que j'ai retenu d'une discussion entre le grand mathématicien Alain Connes et Stanislas Dehaene du Collège de France. A.C. La vraie compréhension d'une démonstration, c'est quand elle est zippée en quelque chose qui n'a plus de temps. Il n'y a plus d'épaisseur temporelle. S.D. Et par contre on le voit. A.C et S.D. D'où image mentale. A.C. C’est le moment où l’objet de pensée n’existe plus au niveau du temps mais au niveau de l’image mentale. Voilà, me semble-t-il, ce qui sépare le réflexe de l'automatisme raisonné qui est en fait une démonstration. C'est la réception, dans ma boîte à lettres, d'un courrier émanant d'une société privée d'accompagnement scolaire dont je tairai le nom, qui m'a conduit à créer cette page. 
Je suis à la retraite depuis plus de 20 ans et je me demande quelles tables on présente dans les écoles en 2019-2020 ? Je suis très inquiet quand je consulte les livres scolaires. Les auteurs sont souvent des professeurs de mathématiques agrégés qui n'ont aucune pratique des classes primaires. En Algèbre, dans (3x4) sans unité et sans signe égal, on peut dire indifféremment 3 fois 4 ou 4 fois 3. En primaire, en arithmétique, il faut, d'abord, donner un sens concret à chaque opération, à chaque calcul. C'était le principal défaut des mathématiques modernes. Trop peu d'élèves pouvaient entrer si prématurément dans l'abstraction.
« Un problème est une histoire. Résoudre un problème c'est être capable de raconter cette histoire. » disait-on autrefois. Quand je demandais à un enfant de me raconter une histoire d'œufs et de nids traduisant l'opération 2 x 3 = 6, il me dessinait 3 nids contenant chacun 2 œufs. 2 nids contenant chacun 3 œufs c'est une autre histoire, même si la récolte de la fermière est la même.
Soit le problème « Combien y a-t-il de crayons dans 25 boîtes contenant chacune 4 crayons ? » Si je me contente d'écrire nb=4x25=25x4=100, il n'y a aucun raisonnement. C'est abstrait. C'est une réponse mécanique, algébrique. C'est l'expression raillée par Vladimir Arnold. Pour moi, aucun doute, concrètement, la réponse est 25 fois 4 crayons donc (4 crayons x 25) puis (4x25). C'est à dire l'opérateur (x25). Je peux dessiner les 25 boîtes, 25 ensembles horizontaux ou verticaux. L'opération 4 fois 25 n'a rien à voir avec notre problème. Je ne vois pas quoi dessiner. 4 ensembles de 25 éléments chacun ne correspond pas au problème. Mais, pour le calcul, je poserai l'opération avec 25 en haut, à la place du multiplicande. Ou mieux, par décompositions multiplicatives, j'obtiens 4x25=2x2x5x5=(5x2)x(5x2)=10x10=100. Pour le calcul en ligne, je peux très bien dire 4x25= (4 fois 20)+( 4 fois 5)=80+20=100 car (4x25)=(25x4) Ici, la commutativité n'intervient pas dans le raisonnement, mais dans le calcul. Il ne faut pas mettre la charrue avant les bœufs. Il faut réfléchir, avant d'agir ! Quelle est la solution la plus avantageuse ? Calcul posé? Calcul mental ou calcul en ligne ? Tout dépend des nombres et du problème posé. Le Les pédagogues modernes prétendent que la connaissance du calcul posé nuit au calcul mental. C'est faux ! (Voir les travaux de Olivier Houdé et ceux-ci correspondent à mon expérience personnelle.) Il faut entraîner les enfants à inhiber les automatismes de l'opération posée et à faire le meilleur choix parmi les nombreux types d'algorithmes opératoires possibles, à optimiser, à toujours rechercher l'excellence. Autrefois, au certif, on ne posait que les opérations qu'on ne pouvait pas faire de tête. Je le sais, j'ai préparé des élèves à cet examen. On favorisait déjà le calcul en ligne. Et, bien avant, le 15 janvier 1936, mon frère, âgé de 10 ans, n'avait pas de calculatrice. Recherchez ses opérations. Notez la difficulté des problèmes et voyez comment il procédait pour calculer. Il posait des opérations pour justifier ou expliquer son calcul mental !
On ne peut faire des progrès en mathématiques que si tout le monde parle le même langage, avec les mêmes conventions clairement établies et affichées. Il y a autant de méthodes d'apprentissage que de livres, et elles sont souvent contradictoires: La bataille des EGOS. Il faudrait penser aux enfants qui changent de classe, d'école.... Je pense aussi aux parents qui tentent d'aider leurs enfants... S'ils font lire les lignes dans un sens différent de celui pratiqué à l'école, ils vont embrouiller leur enfant, pour qui le sens de la multiplication, et de la division, sera incompréhensible.
Avant 1970, j'avais une classe à 4 niveaux(CE2-CM1-CM2-FE). Dans la division de fin d'études, il ne restait pas grand monde. Les meilleurs élèves de 14 ans étaient déjà au collège. Or, tous mes élèves, sans exception, obtinrent le certificat d'études primaires. Dans chaque famille, il y avait toujours quelqu'un capable d'aider l'enfant à résoudre un problème difficile. Ensuite, on ferma ces classes de F.E. et les élèves les plus faibles passaient dans d'horribles classes de 6e qui n'avaient de transition que le nom. À l'arrivée des mathématiques modernes, les parents étaient complètement noyés. Les plus humbles intellectuellement, pouvaient encore aider leurs enfants à apprendre les tables de multiplication et les techniques opératoires. Aujourd'hui, en France, les classes sociales les plus défavorisées sont totalement hors circuit.
Ma méthode d'apprentissage des tables de multiplication ne devait pas être trop mauvaise. Aujourd'hui, les enfants de Singapour, à l'âge du CE2, mémorisent les mêmes schémas. Ils utilisent aussi la notion de machines des mathématiques modernes (Livre CE2 page 70). Et ils ne sont pas trop mal classés dans la compétition internationale.
20 pages de leur livre de CE2, sur 195, sont consacrées aux tables de multiplication par 6,7,8 et 9 (multiplier et diviser). Dommage pour mes élèves qu'ils n'aient pas pu disposer d'un livre d'une telle qualité.
Sinon, pourquoi aller chercher à l'étranger, ce que les vieux instituteurs faisaient mieux autrefois, dans le respect des traditions calculatoires françaises ?
Il y a toutes les subtilités des langues, qu'il est difficile de traduire. On ne mémorise pas verbalement ses tables à Singapour comme en France ! Je ne sais pas si à Singapour on roule à gauche, par contre, l'enseignement y est dispensé en Anglais, et on y récite les tables comme en Angleterre. L'anglais est ma troisième langue. Je ne voudrais pas déformer les écrits des pédagogues de Singapour. Voici ce que je lis:
Learning the times tables is key to mastering primary school math, as memorisation of the tables support mathematical learning and understanding of multiplication and division. These concepts form the foundation to our mental arithmetic, as well as estimation skills. Research has shown that children become more confident and open to learning new concepts once they have mastered the times tables.
Imaginez les difficultés pour les petits mandarins, malais, tamouls, habitués à réfléchir dans leur langue maternelle et qui doivent maintenant, calculer mentalement, automatiser dans la langue de Shakespeare. En France, il n'y a qu'un breton pour le comprendre. La solution, ce sont les schémas visuels.
Voilà une image qu'on ne trouve dans aucun livre français. À TIMSS ADVANCED 1995, c'est la France qui était en tête. En 1995, les résultats des élèves français de CM1 ne devaient déjà pas être trop bons, car c'est à partir de 1988 que les performances avaient commencé à s'effondrer. On ne peut comparer que ce qui est comparable. La soustraction et la division traditionnelles françaises, permettaient à nos enfants d'être très performants en calcul. Voici le schéma qui est l'un des atouts de Singapour, pour résoudre des problèmes. Le même schéma sert à représenter la multiplication et la division
Michel Fayol devrait lire ce qu'écrit Stanislas Dehaene sur le rôle du sommeil dans la mémorisation. Voici un extrait du petit opuscule publié par le journal Le Point : « Acquérir les fondamentaux grâce au meilleur enseignement du monde. »
Le caractère multiculturel de la société singapourienne a aussi paradoxalement donné un coup de pouce à l'innovation pédagogique en maths.
« Nous avons essayé de réduire au maximum l'usage du langage dans l'énonciation des problèmes pour favoriser le visuel, afin de réduire les malentendus pour les élèves dont la langue maternelle n'est souvent pas l'anglais. » explique Lee Fei Chen, éditrice en chef chez Times Publishing. Avant de penser à former les professeurs des écoles, un ministre de l'éducation soucieux de faire progresser les petits Français, devrait, d'abord, recycler les formateurs de formateurs, les inspecteurs, et revoir à la hausse les programmes de mathématiques, en s'inspirant, au minimum, de ceux de Singapour. Et qu'on arrête de culpabiliser les professeurs des écoles ! Ils ne peuvent mettre en pratique que ce qu'on veut bien leur apprendre. Ils ont fait des études supérieures. Moi, je n'ai qu'un bac «sciences expérimentales.» Mais comme ceux qui font la pluie et le beau temps à l'éducation nationale, sont souvent les auteurs des livres scolaires médiocres, contradictoires, imposés aux élèves et à leurs maîtres, qui ne changeront pas d'un iota, et qui ont même l'outrecuidance de venir faire la leçon aux pédagogues de Singapour, on n'est pas près de combler le fossé abyssal qui sépare la France de la tête du classement.
Je trouve aberrant que les formateurs français abordent la multiplication et la division par deux voies intellectuelles différentes et séparément, l'une après l'autre, la division à la Saint-Glinglin.
Pour la multiplication, ils placent indifféremment les deux facteurs par rapport au signe x. Donc, les enfants ne voient pas les deux sens différents des problèmes. Par contre, ils attachent une énorme importance aux deux sens (partition et quotition) de la division, ce qui entraîne le report de l'apprentissage des techniques opératoires à plus tard, des techniques parfois farfelues en terme de rapidité calculatoire. À Singapour, comme dans ma méthode de « L'école libératrice », on fait très attention à la position de l'opérateur dans la multiplication (livre de CE2), ce qui permet de bien comprendre les problèmes multiplicatifs. Pour la division, c'est par la preuve, la commutativité de la multiplication, que l'on peut introduire très tôt la technique opératoire. Les deux sens (quotition et partition) sont compris beaucoup plus facilement car les enfants apprennent simultanément les tables de multiplication et de division. Ils comprennent plus facilement les problèmes, car ils reposent sur des petits nombres qu'ils peuvent manipuler concrètement. Les schémas de la multiplication et de la division sont les mêmes.
La table de Pythagore De nombreux éditeurs, et même la très sérieuse revue "Tangente", commencent l'apprentissage des tables de multiplication en présentant la table de Pythagore que l'élève devra apprendre par cœur. Où sont les images mentales, le sens des problèmes ?. Cette manière de mémoriser, c'est du dressage !Sa symétrie témoigne de la commutativité de la multiplication, mais ne l'explique pas. Tout le monde n'a pas le quotient intellectuel du fils de l'ami d'Arnold, un papa mathématicien... Or, c'est simple à faire comprendre, quand l'enfant peut manipuler méthodiquement, table par table, ligne par ligne, problème par problème, schéma par schéma. Dans un problème arithmétique multiplicatif simple, il y a un nombre concret, le multiplicande, et un nombre abstrait, le multiplicateur. En débutant par la table de Pythagore, on fait intervenir deux nombres abstraits. Les enfants les plus faibles ne vont rien comprendre. Ils vont apprendre bêtement. Il ne faut pas mettre la charrue avant les bœufs. Quant à moi, je faisais construire cette table, à la fin, uniquement pour réviser, consolider les acquis.
La table de Pythagore et les "trucs" ne sont vraiment utiles qu'à ceux qui ont d'abord compris les tables de multiplication apprises méthodiquement, dans l'ordre, problème par problème.
La généralisation de l'usage de la table de Pythagore est apparue avec les maths modernes. Toujours visible, elle devait soulager la mémoire de l'enfant dans les calculs. Et à force de l'utiliser, on parvenait à mémoriser les tables. Mais autrefois, on faisait tellement d'opérations, (c'était indispensable) que tout le monde finissait par savoir ses tables par cœur. Cela a fonctionné tant qu'on a continué à faire beaucoup d'opérations, jusqu'en 1992. La table de Pythagore a été la première prothèse cérébrale fournie aux enfants, tout comme la règle numérique en papier que les instituteurs furent contraints de coller sur la table de chaque élève. La calculatrice a suivi. Des solutions artificielles de facilité trompeuse qui détournent l'enfant de faire l'effort de raisonner pour mémoriser. Et, évidemment, comme le nombre d'opérations à résoudre manuellement a baissé, il est logique que les adolescents ne sachent plus leurs tables de multiplication. Et ils ne pourront pas les reconstruire, faute d'images mentales et de repères. La méthode de l'école libératrice permettait de structurer l'apprentissage par cœur des tables de multiplication et de division. Maths à l'école primaire : Des scientifiques réagissent Voici le problème qui est la cause de leurs profondes réflexions:
La directrice de l'école a 87 lettres à envoyer. Elle doit mettre un timbre sur chaque lettre. Les timbres sont vendus par carnets de dix timbres.
Combien de carnets doit-elle acheter ? Voici maintenant ma solution : Á Singapour, on ne dissocie pas, l'apprentissage des tables de multiplication, des tables de division. (Titre d'une leçon: Multiplier et diviser par 7).
Mais le schéma de l'école libératrice 1967
Il est important que, dès le début de leur apprentissage, les tables de multiplication soient « mobiles », ce qui signifie:
- qu'on évite toute répétition « ordonnée » (du type 2 x 1, 2 x 2, 2 x 3...); - qu'on mêle plusieurs formulations (aussi bien 2 fois 5 que 5 fois 2 pour la table de 2); Ils rejettent ce qui fonctionne à merveille à Singapour. C'est en observant les schémas, différents, de 2 fois 5 et 5 fois 2, que l'enfant apprendra à mémoriser le plus simple, 2 fois les doigts de la main, ou le domino double 5. Apprendre les tables de multiplication, ce ne doit pas être du dressage ! La recherche du quotient, avec un diviseur de deux chiffres, par tâtonnements et encadrements, développait une forme d'intuition dès le CE2. Ne le fait-on pas trop tard aujourd'hui ? Evidemment, ces "grands savants" qui ne savent pas enseigner la table de multiplication par 10, retardent l'apprentissage de la division et on trouve encore les tables de multiplication à la première page du livre de mathématiques de 6e ! Avec les nouveaux programmes ce sera en 5e. On retarde encore l'échéance d'un an ! La mémorisation des tables de multiplication est liée à l'apprentissage de la division euclidienne. Les nombres à retenir sont des repères dans la suite des nombres, des bornes d'intervalles. On ne connaît vraiment les tables de multiplication que lorsqu'on sait les utiliser pour la division. Voici un programme à mettre entre toutes les mains.
Mais pour savoir ce qui se fait réellement à Singapour, le mieux est d'aller directement à Singapour et de faire la traduction soi-même. Progression à Singapour (dès la page 57 du manuel de l'élève ) au CE2:
Dans la nouvelle version du livre de la librairie des écoles, la première potence, c'est (82:4) à la page 92. Ce n'est pas mieux que (67:3). On met la charrue avant les bœufs.
Cette technique opératoire fait suite à l'apprentissage des tables de multiplication, alors que dans le livre préfacé par Laurent Laffforgue, elle les précédait. Cela permettait d'avoir une potence pour un quotient à un chiffre, de verbaliser la procédure de la division avec reste non nul et de mémoriser les tables. Dans la langue française, on a besoin de la table de multiplication et de la table des multiples pour comprendre le sens concret de chaque problème posé. Cette américanisation du calcul est une grosse faute pédagogique. La nouvelle progression ne me convient pas du tout. On apprend les tables de multiplication par 6 puis par 7 (5 leçons). Ensuite, c'est la division par 6 et par 7. (2 leçons) Puis on apprend les tables de multiplication par 8 et par 9 (4 leçons). Enfin on passe aux divisions par 8 et par 9 (2 leçons). On passe du coq à l'âne. La division n'est plus le pendant de la multiplication. Et la première potence c'est encore plus tard. Quelle différence avec la première version ! où l'on étudiait la multiplication et la division en même temps. À Singapour, on pose la soustraction. C'est plus facile. On évite l'écueil de la mémorisation de la soustraction. On se concentre sur l'algorithme. Mais plus tard, on sera moins virtuose. (9:2); (12:2) (28:2); (34:2); (73:2) (400:2); (500:2); (550:2); Révision des tables par 3; 4; 5 (96:4); (80:3); (426:3); (823:4) Ce n'est qu'ensuite qu'on procédera à des divisions par 6;7;8;9 au moment de l'apprentissage de ces tables de multiplication. Je suis stupéfait que des "scientifiques" aussi réputés ne sachent pas que la mémorisation des schémas doit précéder le «drill», et surtout qu'ils n'arrivent pas à se mettre au niveau des enfants. Pas étonnant que les enfants qui utilisent ces livres ne sachent pas grand chose de la division et soient si mal classés dans les épreuves internationales. Dans l'un des livres on apprend par cœur la table de Pythagore, et dans l'autre, ce sont toutes les lignes les plus difficiles de cinq tables que l'enfant doit mémoriser de façon concentrée. En neurosciences, on semble découvrir ce que les vieux instituteurs pratiquaient tous les jours. Et comme ces découvertes, qui enfoncent des portes ouvertes, contredisent souvent les formateurs français, ceux-ci entrent en conflit avec ces nouveaux savants. Et on dit qu'il n'y a que les imbéciles qui ne changent pas d'avis.
Dans le domaine de l'éducation, les enseignants doivent maintenir un haut niveau d'attention chez l'élève en stimulant, en rendant le cours attractif et en concentrant l'élève sur une seule tâche.
Jean Jacques Bourdin vient de tenter de prendre en défaut un candidat à la présidence de la république, pour vérifier s'il était nul ou non en maths en lui posant la question « 7 fois 8 ? »
Le candidat a eu l'élégance de répondre :«Imagine-t-on le général De Gaulle répondre à des tables de multiplication?» J'attends avec impatience qu'un grand mathématicien vienne répondre à Jean Jacques Bourdin: « 7 fois 8 c'est 5 fois 8 plus 2 fois 8 », ou en plagiant Vladimir Arnold : « 7 fois 8, c'est 8 fois 7, car la multiplication est commutative. Et, 8 fois 7, c'est 28 plus 28 , c'est à dire 56.» Car au café du commerce, on est persuadé qu'être fort en maths c'est seulement avoir de bons réflexes. Et le pire, c'est que l'un de nos plus grands didacticiens aurait pu ajouter que le futur président de la république ne maîtriserait pas le socle. L'un de nos plus brillants didacticiens est persuadé que Didier Migaud ne connaît pas ses tables de multiplication. Et de railler que Didier Migaud ne maîtriserait pas le socle ! La cour des comptes devrait se pencher sur le rôle destructeur de nos "experts" qui n'ont jamais eu la responsabilité de classes d'enfants de 8 ans, et qui perpétuent à croire et à propager, que connaître les tables de multiplication, c'est uniquement, pouvoir les sortir bêtement. Si Didier Migaud était revanchard, il devrait réclamer une compétition à ses arrogants détracteurs, une fiche de calcul rapide écrite. Je persiste et signe. Tous ces formateurs haut placés, qui se sont moqués de Didier Migaud, devraient être recyclés avant de continuer à animer des formations de calcul mental.
« Il est très important de s'entraîner suffisamment pour automatiser des réflexes, et le calcul mental est un de ces réflexes qu'il faut avoir. »,
C'est le réflexe conditionné de Pavlov. avait déclaré notre jeune ministre de l'éducation nationale, conquise par ces "scientifiques" et ces "experts". Un enfant n'est pas un animal. Moi, j'automatiserais plutôt un algorithme que l'enfant a compris. La répétition le transformera, peut-être, en réflexe, mais j'essaierais surtout d'éviter les mauvais réflexes. Un raisonnement, au départ laborieux, finit par devenir « spontané ». Automatiser un réflexe n'a pas de sens. Un réflexe, on l'a, à vie. On ne peut pas le modifier. On ne crée que des réflexes en apprenant par cœur la table de Pythagore. Et là, c'est du dressage. Les exercices de ce type foisonnent sur Internet. Ils excitent les enfants qui réussissent et qui aiment la compétition, mais ils desservent tous les autres. Les enfants qui échouent, pourront-ils un jour, aimer les mathématiques ? Autrefois, tout exercice donné devait être corrigé. Les auteurs de logiciels sont, rarement, des instituteurs. « Le bon maître ne punit jamais, il encourage toujours... » m'a-t-on appris autrefois. Or, la bonne compréhension des tables de multiplication (et de division, surtout) est une des clés de la réussite future en calcul, puis en mathématiques. À Singapour, 20 pages de leur livre de CE2, sur 195, sont consacrées à l'apprentissage des tables de multiplication par 6,7,8 et 9 (multiplier et diviser). Ouvrez un livre français, et comparez ! On rédige un nouveau programme à la hauteur des compétences des plus jeunes enseignants français, déjà formatés par les mêmes "scientifiques" et les mêmes "experts". Ils gomment toute la dimension du sens. Ils associent l'élève à un « automath ». Leur division, c'est l'opération escargot. Retarder l'apprentissage de la division par un nombre de un chiffre, au CM1, c'est R I D I C U L E !!! Lorsqu'on prend tant de retard dès le plus jeune âge, qu'on n'a pas pris l'habitude de mémoriser intelligemment (le seul résultat et non un algorithme complet menant au résultat), il sera difficile, plus tard, de retrouver des formules de trigonométrie, par exemple. Et on les appliquera mécaniquement. Une jeune étudiante asiatique "chambre" gentiment ses camarades français. Elle a une image mentale, pour chaque formule, là, où les jeunes Français n'ont qu'un réflexe, bêtement mémorisé.
« Quand je suis arrivée en France, j'ai pu constater que j'avais beaucoup d'avance par rapport à mes camarades français, grâce à mes études secondaires à Shanghaï.
Par exemple sur les formules trigonométriques. Nous on les avait étudiées en collège, alors qu'en prépa, les élèves Français ne savent pas le faire, et ont trouvé très difficile de les trouver. C'est vraiment une montagne pour eux de connaître toutes les formules. Alors que pour nous c'était vraiment facile.»
« Lorsqu'il regarde des formules mathématiques, ce n'est pas la formule mathématique que voit le mathématicien : il fait un lien absolument instantané avec ce qu'il a construit dans sa tête, et il n'a pu construire cette image mentale que par un acte actif, pas de manière passive.» (Alain Connes)
J'ai été agréablement surpris en écoutant notre nouveau ministre de l'éducation nationale:
La compétition exacerbée qui règne dans ces pays ne conviendra sans doute pas chez nous. Aujourd'hui, à Singapour, les parents s'impliquent et peuvent aider leurs enfants. Ils comprennent ce qu'on demande. En appliquant les directives de l'OCDE, cela sera-t-il encore possible plus tard ? J'ai bien peur que dans quelques années, ce pays se retrouve à un niveau aussi médiocre que le nôtre. Le jour où seuls les parents aisés pourront payer des cours particuliers, comme en France. On trouvera ici, les valeurs que j'ai essayé de transmettre, tout au long de ma vie:  Les valeurs de Stéphane Diagana. Les valeurs de Stéphane Diagana.
En France, cette saine émulation, est devenue un privilège réservé aux riches. La compétition, ce n'est pas la guerre ! Moi, fils de "gueule bleue", je n'ai pas oublié d'où je viens.
J'ai pour habitude de comparer l'apprentissage du calcul mental à l'initiation au tennis de table. Il y a beaucoup de similitudes.
Mes remarques ne plaisent pas à tout le monde. Un "pédagogue" a eu des paroles injurieuses, alors qu'il ne connaît absolument rien à ce sport. J'ai tout de même une certaine expertise de la pré-initiation et de l'initiation des jeunes enfants, reconnue par mes pairs et je suis désolé, pour justifier ce savoir, de devoir manquer un peu d'humilité. En calcul, comme dans tous les sports, on apprend d'abord les gestes de base, et ce qui est important, les gestes qui sont appris sans faute, pour préserver le perfectionnement dans l'avenir.
*
* * * * *
 Cliquez ici : Cliquez ici :C'est la première étape de mon solveur de divisions, un robot qui permettrait de faire gagner trois années, dès le CE2, aux élèves de nos "scientifiques". Cette première marche est primordiale, capitale. Il ne faut pas la rater. Elle détermine toute la suite, que l'enfant sera à l'aise ou non, en calcul. Aujourd'hui, je m'appuierais sur la mémoire auditive pour le par cœur, avec l'aide des nouvelles technologies.  Voici comment je créerais mes fichiers. Voici comment je créerais mes fichiers.
Apprendre la technique opératoire de la division était chronophage. Cet apprentissage était indispensable, absolument nécessaire, au 20e siècle. Les concepteurs de programmes, à l'heure des calculatrices, sont tentés de reporter à plus tard cet apprentissage et on prive les enfants du 21e siècle, de la compréhension du sens de la division, de la recherche dichotomique avec ses repères essentiels. Pourquoi était-ce long et difficile ? Tout simplement, parce que les élèves les plus faibles, n'ayant pas encore tout à fait acquis les automatismes de calcul, (tables, soustractions) se perdaient dans le cheminement vers le résultat. C'était un cercle vicieux. Lors de mes dernières années d'enseignement, j'avais une classe de CE2 où près de la moitié de mes élèves étaient suivis par le RASED. Certains avaient 3 à 4 années de retard. S'il n'a que deux ou trois élèves en difficulté, un maître expérimenté sait individualiser son enseignement. Impossible donc, d'individualiser. Où trouver le temps nécessaire, le moment propice ? J'eus l'idée d'inventer une sorte de robot qui corrigerait à ma place. On sépare les difficultés. Le plus important, c'est l'algorithme. On utilise les aides calculatoires à bon escient. Et cela avait marché. Tous les élèves, sans exception, comprirent rapidement la démarche opératoire et ensuite, ils firent de moins en moins d'erreurs de calcul. Cette idée m'avait été inspirée par mes connaissances et mon expérience d'entraîneur de tennis de table. Avec un robot lanceur de balles, on fixe, de façon durable, un geste de base, en quelques minutes, alors qu'il fallait, avant, des heures et des heures de répétitions monotones pour arriver à un résultat parfois décevant. J'ai écrit un programme d'extraction de racine carrée sur le même concept.  Mon robot d'extraction de racine carrée Mon robot d'extraction de racine carréeDans un problème du Brevet 2014, de type écologique d'économie d'énergie avec des bottes de paille, on devait trouver la racine carrée de 20,25 mē. Problème trop difficile, de l'avis des candidats. Je connais l'algorithme manuel et je sais que la difficulté, autrefois, était la partie calculatoire où tout le monde se trompait. Moi, je n'utilise que la première étape. Et je sais que le chiffre du nombre entier sera 4 (diagonale de la table de Pythagore). Le premier chiffre de la partie décimale, je l'ai par tâtonnements et mon intuition me dit que c'est 5. J'utilise la calculatrice pour vérifier que 4,5 fois 4,5 font 20,25. J'ai une image mentale du théorème de Pythagore que n'ont plus les jeunes d'aujourd'hui, à qui on a appris, à se contenter d'appuyer sur une touche de leur calculette, pour trouver le résultat.
*
Autrefois, on utilisait un dictionnaire pour rechercher le sens, la nature d'un mot nouveau, vérifier l'orthographe. On recherchait par encadrements dans la liste des lettres de l'alphabet (entre 2 bornes). C'était un exercice mathématique qu'il faudrait aujourd'hui faire connaître à l'enfant avant de lui permettre de faire une recherche sur Internet. On trouve aussi le quotient par encadrements dans la division.* * * * * Il n'y a que des gens médiocres en pédagogie qui ne voient pas l'importance de la recherche dichotomique.
Voici deux petits programmes personnels de recherche par encadrements.
 Recherche d'une lettre de l'alphabet Recherche d'une lettre de l'alphabet Recherche d'un nombre (Vous pouvez choisir vous-même la plage de recherche.) Recherche d'un nombre (Vous pouvez choisir vous-même la plage de recherche.)
Les problèmes
« Devenir intelligent c'est, bien-sûr apprendre à raisonner juste. Mais c'est tout autant apprendre à ne pas raisonner faux. C'est ce que révèlent les neurosciences, avec l'appui de l'imagerie cérébrale. L' « âge de raison » apparaît ainsi sous un nouveau jour : ce qui se joue vers 7 ans, c'est surtout l'émergence chez l'enfant de la capacité à choisir entre différentes stratégies cognitives, et à inhiber les réponses automatiques mais fausses. »
(Olivier Houdé -Revue La Recherche novembre 2011)
L'exemple de Didier Migaud le démontre, on reproduit machinalement un acte réflexe. Les fameuses « situations-problèmes » de la pédagogie dite moderne, me semblent être traitées avec beaucoup de désinvolture au cours élémentaire, et surtout, avant. Faire tâtonner l'élève, rechercher par investigation, j'approuve; mais je n'aurais jamais validé, formalisé, une réponse fausse ou tortueuse. Il y a un risque de créer un mauvais réflexe. L'enfant doit être orienté vers le meilleur algorithme afin qu'il puisse inhiber les mauvais. Il faut l'entraîner à faire le bon choix, à toujours, rechercher l'excellence. Ou, comme on le dit en informatique, à optimiser. Le cheminement inverse est dangereux. Ce n'est pas en gavant un enfant de situations-problèmes où il construit seul son savoir, qu'on va le rendre plus intelligent. Ce qui peut marcher avec d'autres sciences produira des effets désastreux en mathématiques. Si une réponse experte n'a pas été formulée, le maître, en désespoir de cause, doit l'expliciter. Sinon, les parents finiront, ou non, le travail, en fonction de leurs connaissances : C'est une discrimination négative.  Avis du doyen de la faculté des sciences de l'éducation (Helsinki - Finlande) Avis du doyen de la faculté des sciences de l'éducation (Helsinki - Finlande)
J'ai confiance dans les progrès de la recherche scientifique, et de leurs nouveaux instruments d'investigation cérébrale. Il faudrait que les pédagogues en tiennent compte, dialoguent avec les chercheurs et se remettent en question.
« Il n'y a que les imbéciles qui ne changent pas d'avis.
* * * * * * 
Voici le problème qui a été posé, en 1997, par un jeune inspecteur lors d'une conférence pédagogique, pour nous présenter les «situations-problèmes». C'était l'année de ma dernière classe. Absolument personne n'avait trouvé la solution. Les vieux instituteurs avaient été les moins mauvais. J'ai retrouvé ce même problème, par hasard, sur le site de l'inspection académique, en 2007, toujours pour présenter les « situations-problèmes ». On manque d'imagination. Et on n'explique toujours pas la solution. Mais la finalité doit être la même. Et vous, ami qui visitez mon site, quelle est votre solution ? Cinq minutes pour répondre comme à notre examen.  Voir ma solution Voir ma solution Si vous avez une solution plus élégante, merci de me la faire connaître.  Un exercice d'application Un exercice d'applicationVoilà comment, on nous dépréciait, on nous culpabilisait. «Vous verrez, les enfants feront mieux que vous!» Evidemment, pour ce type de problème stupide, on a plus de chances d'avoir la bonne réponse en se remettant au hasard qu'en réfléchissant.
*
Voici, maintenant, un autre problème qui a fait le buzz, sur Internet, en l'été 2015:
* * * * *
Dans le train entre Narbonne et Toulouse, à l'arrêt de Carcassonne, quatre-vingt-sept passagers descendent. Il y a à présent cent soixante-quinze passagers dans le train.
Combien y avait-il de passagers au départ de Narbonne ?  Voir mes sources Voir mes sources
On ne peut pas répondre à la question. J'ose espérer que la coquille est involontaire. Un instituteur n'est pas là pour piéger ses élèves. Ils perdraient confiance en eux, en leur maître. Ils n'oseraient plus répondre à ses questions. Et en plus, on les lance sur une fausse piste, en leur suggérant d'utiliser une calculatrice ! On leur apprend à raisonner faux. Moi, j'aurais posé le problème autrement. J'aurais prévenu les enfants: « Il y a une erreur dans l'énoncé. Retrouvez-la.» Ensuite, j'aurais tenté de leur apprendre à raisonner juste, en leur suggérant une approche algorithmique: découpage du problème en étapes (départ,trajet, arrivée).  Voir ma solution Voir ma solution Il s'agissait, heureusement, d'une simple coquille. Que celui qui n'a jamais gaffé, lui jette la première boulette. Je ne commenterai pas la leçon complète à voir ici :  Voir la vidéo Voir la vidéo
Mais on a là, dans la présentation des questions des deux problèmes (Même erreur dans les 2 problèmes), l'illustration de la méconnaissance de la notion du temps qui passe, si importante en mathématiques, le manque de repères, de bornes d'intervalles. Mais pourquoi personne ne voit ces erreurs? La vidéo date de 2014 ! Je ne saurais trop conseiller, aux éminents membres de cette équipe et à tous ceux qui passent sans remarquer la coquille, de lire les ouvrages recommandés ici :  Editions Buissonnières ou d'apprendre à dessiner Editions Buissonnières ou d'apprendre à dessiner  En BASIC 256 En BASIC 256
Si moi je vois immédiatement la coquille dans l’énoncé, ce n’est pas parce que je suis particulièrement brillant en mathématiques. J’ai tout simplement réfléchi selon la méthode que j’ai toujours appliquée dans ma classe. Celle que m’avait transmise mon excellent maître, monsieur Berthélémé. « Comment vais-je mettre sur la voie les enfants qui sont perdus ? Quels sont les repères spatio-temporels sur lesquels je vais pouvoir m’appuyer ? » J’aurais fait tracer l’itinéraire, à la craie, sur la carte murale. J’aurais fait marquer les gares. Et là, je vois l’erreur de borne d’intervalle. Il peut s'en passer des choses entre Narbonne et Carcassonne... Il devrait y avoir une bonne demi-heure de voyage... Comme je ne connais pas bien cette région, je vais sur le site Internet de la SNCF... Et là je vois qu'il y a même un arrêt entre les deux gares: Lézignan, où des voyageurs peuvent monter, d'autres descendre. Je me suis d’ailleurs demandé si ce problème n’était pas une farce. Tous les commentateurs de Neoprofs sont tombés dans le panneau comme un seul homme.  Voir aussi ce qu'en pense Olivier Houdé, un grand scientifique, ancien instituteur. Voir aussi ce qu'en pense Olivier Houdé, un grand scientifique, ancien instituteur.
*
D'un côté: 2mn de recherche individuelle, 10mn de recherche en groupes (calculatrice autorisée), à cela s'ajoute un temps indéterminé de comparaison des résultats, pour un seul problème.
La France est l'un des pays qui consacre le plus de temps aux fondamentaux.* * * * *  Pendant ce temps au concours du Kangourou des mathématiques Pendant ce temps au concours du Kangourou des mathématiques
L'épreuve doit être individuelle et sans calculatrice. 26 problèmes en 50mn. Le lauréat national de l'un des concours est un voisin. Papa et maman sont ingénieurs, pépé était professeur de mathématiques. On aura beau diminuer les difficultés des problèmes, abaisser le niveau des exigences, l'école sera toujours, et de plus en plus inégalitaire. Quelle loi peut empêcher un grand-père d'aider son petit-fils ? Le programme, il s'en fiche éperdument ! Et il ne prépare pas spécifiquement ce concours-là.
*
Il arrive à Roland Goigoux de contester Stanislas Dehaene, et ici, apparemment, à juste titre. * * * * *  Voir Voir
Les méta-analyses des « Evidence Based » (données fondées sur la preuve) comparent les résultats des recherches pour évaluer celles qui sont jugées « scientifiques » et les synthétisent. Ainsi, en 2011, on a pu conclure que :
Roland Goigoux fait l'apologie de la méthode que j'ai utilisée pour l'apprentissage des tables de multiplication, des techniques opératoires et la résolution de nombreux problèmes. Mais quel type de démarches, le réseau Canopé donne-t-il en modèle à ses nombreux visiteurs ? Ce sont les démarches fondées sur le tâtonnement ouvert sans guidage, des méthodes chronophages. Pourquoi ne propose-t-on pas, aussi, celles qui donnent les meilleurs résultats ? Et on s'étonne que la France ne brille pas dans les comparaisons internationales, bien que les petits Français passent plus de temps que les meilleurs à faire des mathématiques. Il suffit de lire le livre du maître Eiller CE2 de 1980, pour comprendre pourquoi les vieux instituteurs utilisaient un second livre en parallèle. Les enfants, surtout les plus faibles, ont besoin d'être guidés. Ils ne trouveront pas les repères tout seuls. Dans un travail de recherche en groupe, l'enfant qui aura trouvé, ne laissera pas d'illusion à ses camarades.
*
Problème alternatif pour élèves de même niveau en 1975. - MATHÉMATIQUE au C.M. (Postel SUDEL) -
* * * * *
Un matin, au départ, il n'y a dans un autobus que le chauffeur et le receveur.
Au 1er arrêt, 11 personnes montent. Au 2e arrêt, 2 personnes descendent, 5 personnes montent. Au 3e arrêt, 0 personne descend , 4 personnes montent. Au 4e arrêt, 3 personnes descendent, 18 personnes montent. a) Établissez une chaîne d'opérateurs que vous réduirez ensuite pour trouver le nombre de personnes que transporte l'autobus après le 4e arrêt. b) En partant du 4e arrêt, retrouvez le nombre de personnes transportées du 3e au 4e arrêt, du 2e au 3e, du 1er au 2e.  Voir ma solution Voir ma solution Avec en prime un programme permettant de créer des chaines d'opérateurs.
*
* * * * * Je recommande, à la page http://www.ien-quimper1.ac-rennes.fr/pages/maths.html des problèmes pour chercher, la vidéo. Elle montre l'importance discrète du maître dans la recherche des solutions. Pourvu qu'à la fin, les enfants puissent inhiber les mauvaises réponses et valider, formaliser la meilleure solution. C'est en effet au maître de décider et de démontrer quelle est la meilleure solution. Pour ma part, je serais allé plus loin, jusqu'à l'obtention d'un algorithme qui généralise une solution acceptable. Je ne pense pas que toutes ces manipulations étaient vraiment utiles. Une perte de temps qui ne développe pas le raisonnement mathématique.  Voir ma solution (PHP) Voir ma solution (PHP) Voir ma solution (Canvas - HTML5) Voir ma solution (Canvas - HTML5)Ce qu'il faut bien comprendre, c'est qu'il y a plusieurs types de problèmes. À chacun on appliquera l'une des trois méthodes définies par Roland Goigoux qui correspond au problème posé, ou mieux, les trois savamment dosées. C'est ce qui est remarquable dans la vidéo de Quimper 1
Typologie des problèmes A la page 151 de « La bosse des maths », je lis : « Je pense que l'usage raisonné de la calculatrice, en libérant l'enfant des aspects fastidieux et mécaniques du calcul, peut lui permettre de se concentrer sur le sens ». Avec un ordinateur, on peut faire mieux. On peut jouer avec les nombres, mais aussi et surtout avec les algorithmes. Une calculatrice, c'est une boîte noire (absence totale d'images mentales). Elle ne donne que le résultat. Avec un ordinateur, on écrit des lignes qu'on peut sortir sur une imprimante, étudier, et éventuellement rectifier. Ces lignes, ce sont des suites de codes numériques et alphanumériques. Comme il y a un permis de conduire un véhicule,
« Sans hier et sans demain, aujourd'hui ne vaut rien. »
Qui a tenté de faire résoudre un problème avec l'assistance d'un ordinateur, par un enfant qui a été initié à la programmation ? Moi, je l'avais fait en utilisant le Basic du TO7. Et j'avais constaté que l'enfant acquiert concentration et intuition phénoménales. L'enfant peut s'amuser à résoudre une dizaine de problèmes alors que son voisin, sans assistance, dans le même temps, peine sur un seul. En écrivant son code, il matérialise les algorithmes. Il remplace les manipulations manuelles par la simulation informatique. Il concrétise des raisonnements abstraits. Il multiplie les images mentales qui lui resserviront plus tard. 26 problèmes en 50 minutes, cela devient facile. Et voilà comment on devient lauréat du concours du Kangourou, tandis que les camarades ont droit à un lot de consolation. Aujourd'hui, grâce à BASIC-256, HTML5 (Canvas), ou à EASYPHP ce serait de nouveau possible. Dans son cours, Introduction à l'algorithmique, à l'université Diderot (Paris 7), Christophe Darmangeat affirme: Cependant, et j’insiste sur ce point, les réflexes, cela s’acquiert. Et ce qu’on appelle l’intuition n’est finalement que de l’expérience tellement répétée que le raisonnement, au départ laborieux, finit par devenir « spontané ». Mon expérience personnelle me permet, en effet, de le confirmer. La réponse, à un problème, produite par un programme informatique, est un algorithme que l'on vérifie et que l'on optimise. On ne validera que des réponses exactes. On va donc mémoriser de bons algorithmes et, dès lors, développer effectivement son intuition. Il ne s'agit pas, évidemment, de remplacer la résolution classique de problèmes (la maîtrise des techniques opératoires est nécessaire, indispensable), mais de la compléter, de poursuivre à la maison, ou en activité post-scolaire ce qui a été fait en classe. A l'école, l'instituteur choisit un problème en fonction du niveau moyen de sa classe. Les élèves, les plus faibles, comme les plus forts, s'ennuient. Pour les uns, c'est trop difficile, pour d'autres, c'est trop facile. Avec la programmation informatique en complément, c'est l'excellence pour tous. C'est par les opérateurs des mathématiques modernes, que j'avais pu introduire la résolution de problèmes, assistée par ordinateur. Au départ, une bonne compréhension de toutes les lignes des tables de multiplication (et de division) est donc nécessaire. Attention, le langage Scratch n'a pas, à ma connaissance, d'opérateur de la division euclidienne. L'opérateur des mathématiques modernes est constitué de deux parties, entre parenthèses,( le signe et un nombre ) La flèche indique le sens de l'algorithme.
En arithmétique traditionnelle, on rédigeait la solution d'un problème en 2 lignes. En mathématiques modernes, c'était en 4 lignes.
 Voir ce qu'en pense Olivier Houdé Voir ce qu'en pense Olivier HoudéCalcul mental: Je signale que j'avais commis une coquille dans la première version de mes exercices d'additions (programmes écrits trop rapidement).  Voir ici.
Merci à l'ami Jean-Yvon qui me l'avait rapidement signalée et que j'avais corrigée, le temps d'apprendre à dessiner des opérateurs sous Canvas. Voir ici.
Merci à l'ami Jean-Yvon qui me l'avait rapidement signalée et que j'avais corrigée, le temps d'apprendre à dessiner des opérateurs sous Canvas.
41 + 28 41 + 30 = 71 - 2 = 69 «Il n'est pour voir que l'œil du maître.» Cette ligne choque évidemment un professeur de mathématiques. La coquille, que je ne cherche pas à minimiser, a pour cause, sans doute, la sénescence. En fait, je n'ai jamais procédé de la sorte dans ma classe. J'utilisais les chaînes d'opérateurs (réduction ou décomposition). Et le plus important, n'est-ce pas la mémorisation du schéma ? Et les manipulations, pour les plus faibles ?
Voici, maintenant, comment on fait à Singapour. Il ne manque que le cercle.
Là encore, cette méthode de décomposition recomposition d'opérateurs a disparu du nouveau livre de CE2. On calcule maintenant sur des numéros, ceux de la droite numérique. C'est l'américanisation du calcul. Mais que fait-on réellement à Singapour ? C'est une question à laquelle j'aimerais pouvoir répondre.
Voici une autre disposition, utilisée en 6e par un professeur de mathématiques, qui me convient bien, aussi.
La méthode, ligne par ligne, que l'on rencontre dans l'émission "des chiffres et des lettres", est certainement valable. Je l'avais utilisée, il y a bien longtemps, en 1967, lorsque je préparais des adolescents de quatorze ans au certif. C'est aussi ce que font les professeurs, au collège. Mais, au CE2, à huit ans, ne vaut-il pas mieux éviter le signe égal et les confusions qu'il peut engendrer ? On risque d'embrouiller tous ceux qui ont du mal à passer du concret à l'abstrait. Je serais curieux de savoir, si à Singapour on ne pratique pas la résolution de problèmes assistée par ordinateur que je croyais avoir inventée. Je n'osais pas trop en parler, de peur d'être pris pour un illuminé. Dans ce petit pays, on ne pratique plus la pédagogie du 19e siècle. On comprend d'abord, on mémorise ensuite, et non l'inverse ! On se sert beaucoup des opérateurs des mathématiques modernes (le mot «machine» pour les plus petits). Les chaînes d'opérateurs, en résolution de problèmes, c'est la programmation informatique sans ordinateur. À Singapour on a gardé le meilleur des mathématiques modernes, les opérateurs. En France, on apprend les opérations les unes après les autres, la division trop tard. La notion d'opérateurs inverses permet de démontrer qu'il est préférable de les apprendre simultanément. Est-ce au collège que le professeur va demander à ses élèves de faire des manipulations que les enfants d'autrefois faisaient au cours préparatoire ? Le meilleur moment pour apprendre les différents sens des multiplications et des divisions n'est-il pas au cours élémentaire lorsque les enfants apprennent leurs tables, en jouant avec des petits nombres, des repères qui leur sont familiers ? Lorsque les formateurs français auront l'humilité de reconnaître leurs erreurs, alors, on pourra envisager des progrès. Lorsqu'on compare la méthode de Singapour à ce qu'on faisait autrefois, on peut remarquer des similitudes. La plus importante tient à la mémorisation de schémas de résolution de problèmes. Ce n'est donc pas le par cœur stupide qu'affirment les détracteurs qui défendent leurs méthodes soi-disantes progressistes, mais en réalité, obsolètes et rétrogrades. Année après année, Singapour occupe la première place de toutes les études internationales. Les chercheurs français persistent à présenter et imposer, par leurs manuels scolaires qui se vendent bien, leurs méthodes de dernier de la classe.. Un problème de mathématiques, posé à des lycéens de Singapour, avait mis en émoi les internautes du monde entier, suscitant débats et contestations. Il fut donné à des élèves de 15 et 16 ans dans le cadre d'une olympiade de maths, voici son énoncé :
"Cheryl veut faire deviner la date de son anniversaire à deux nouveaux amis, Albert et Bernard, en ne leur fournissant que de minces indices. Cheryl suggère 10 dates :
les 15, 16 et 19 mai ; le 17 et 18 juin ; le 14 et 16 juillet ; le 14, 15 et 17 août. Cheryl a ensuite dit à Albert le mois, et à Bernard le jour de son anniversaire. Albert affirme ensuite : « Je ne sais pas quand est l'anniversaire de Cheryl mais je sais que Bernard ne sait pas non plus. » Bernard ajoute : « Au départ, je ne savais pas quand était l'anniversaire de Cheryl, mais maintenant je sais. » Albert répond : « Alors je sais aussi quand est l'anniversaire de Cheryl. »  Voir ma solution Voir ma solution
Ce problème n'est pas sans rappeler les problèmes proposés autrefois pour exercer la logique et l'esprit de déduction des candidats au certif. Mais en abuser est contre-productif. Il s'agit de conserver la motivation intacte.
Parts de gâteau:
Mamie Suzanne a préparé un gros gâteau. Elle sort le plat cylindrique du four et démoule le dessert sur une planche. Elle annonce qu'elle va le couper en huit parts égales, en seulement trois coups de couteau. Comment va-t-elle s'y prendre ?  Voir ma solution Voir ma solution
C'est si simple quand on sait. Je dois avouer que je n'avais pas trouvé, seul, la date de naissance de Cheryl. J'ai passé pas mal de temps à comprendre la solution. Mais, si je devais expliquer la solution à quelqu'un, je présenterais ma vérification, qu'on ne trouve pas sur le Web. Souvent, c'est la vérification qui éclaire le sens d'un problème. Des problèmes du livre Larousse, je ne connaissais qu'une toute petite minorité de solutions. Mais lorsqu'on la maitrise, il est possible de la faire découvrir à des enfants. C'est même tout un art de leur laisser l'illusion qu'ils l'ont trouvée eux-mêmes. Et lorsque l'un des parents vient vous dire que leur enfant a essayé de les coller avec votre problème, alors, vous pouvez dire que c'est gagné. En voilà au moins un qui ne détestera pas les maths. Je trouvais cela réjouissant quand c'était un parent de condition sociale modeste qui venait m'en parler. "La stratégie de résolution de problèmes par la « modélisation en barres », caractéristique de la méthode de Singapour, tient du génie", affirment certains journalistes. Alors, je vous recommande d'aller consulter le cahier de compositions de mon frère (10 ans en 1936).  Voir... Voir...
J'ai aussi préparé des enfants au certif en 1967-69 (100% de réussite). Mes élèves, aussi, ont toujours pratiqué cette méthode géniale. Il y a des savoir-faire qui n'ont pas été transmis aux nouvelles générations de professeurs des écoles. La faute à qui ? Voici un problème amusant trouvé par hasard sur un site Internet.
J'élève des araignées (toutes de la même espèce), des poules et des lapins.
Je compte 148 pattes, 26 têtes et 142 yeux...
Puisque aucun de mes animaux n'est mutilé, combien mes araignées ont-elles d'yeux chacune ? Il n'est pas question, pour moi, d'aller apprendre la résolution d'un système d'équations à plusieurs inconnues à un enfant de cycle 3, ni même de lui apprendre la méthode de fausse hypothèse, le problème classique du certif d'autrefois. Mais je tenterais volontiers de lui faire découvrir un algorithme de résolution du problème, à l'aide de schémas ordonnés, de manipulations. Il est plus facile pour un enfant de raisonner sur des petits nombres. On a de meilleurs repères dans son jardin que dans l'océan. On comprend les différents sens des opérations en apprenant ses tables. Le plus grand nombre est 18 (addition, soustraction) et 81 (multiplication, division). Ici, remplaçons {148, 26, 142} par {24,5,18}, par exemple. Ensuite, on va pouvoir résoudre le premier problème car l'algorithme est similaire. Si vous voulez voir comment,  C'est ici : la résolution de problèmes assistée par ordinateur. C'est ici : la résolution de problèmes assistée par ordinateur.Mais je donne aussi des exemples de problèmes plus simples. Mes exemples (PHP - Basic 256 - Small Basic - Scratch - JavaScript)
Si vous préférez voir et écouter que lire  c'est vers là.... c'est vers là....
Quel ministre de l'éducation nationale est l'auteur de ce texte ?
Il fallait revisiter le système éducatif, et commencer par le début, l'école primaire. C'est là en effet que se forge et se construit l'esprit des enfants. C'est là qu'ils prennent leur élan et que s'installe cette volonté de réussir qui les accompagnera tout au long de leur scolarité et les aidera à rebondir à tout âge de la vie.
L'égalité des chances est le premier pari, qu'il nous faut gagner en permanence - et dès le début. L'autre pari se nomme excellence : l'égalité des chances se construit par le haut. Elle signifie l'excellence pour tous, c'est-à-dire donner le meilleur à chaque enfant.  Quelques programmes de calcul mental Quelques programmes de calcul mental
 Page d'accueil Page d'accueil | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


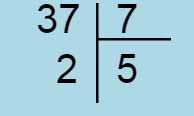
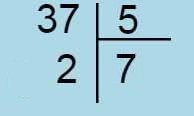




 haut de la page
haut de la page