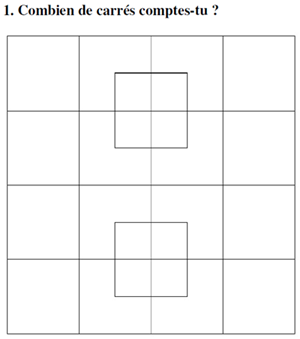
Je compte les carrés de côté 1/2, il y en a 8
puis ceux de côté 1, il y en a 4x4+2 ;
ensuite, pour ceux de côté 2,3,4 on peut faire comme s'il n'y avait qu'un quadrillage 4x4 (quadrilatères réguliers).
pour les carrés de côté 2, on peut regarder les possibilités pour le sommet en haut à gauche, il y en a 3x3,
puis pour les carrés de côté 3, il y en a 2x2,
et il n'y a enfin qu'1seul carré de côté 4.
8 + 18 + 9 +4 +1 =40 ou ( 8 + 2 +(1 x 1)+(2 x 2)+(3 x 3)+(4 x 4))=40
Au total donc 40 carrés.
Cette solution est évidemment trop abstraite pour un enfant.
En classe, j'aurais commencé par des manipulations. J'aurais donné aux enfants plusieurs exemplaires de problèmes et une paire de ciseaux.
Première étape: déterminer les carrés par rapport à leur taille, en les découpant dans les énoncés: 5 modèles.
Deuxième étape: pour chaque modèle, le faire glisser méthodiquement, de gauche à droite, du haut vers le bas.
Je ne vais pas les détailler ici, mais j'aurais posé des questions aux élèves pour les mettre sur la bonne voie et leur laisser l'impression qu'ils trouvent seuls la bonne solution.
Théorie des nombres :  Algorithme
Algorithme
Algorithme: (2n3 + 3n2 + n) / 6

 Algorithme
Algorithme