|
LA SOUSTRACTION
À l'examen d'entrée en 6e, autrefois, l'épreuve de calcul comprenait un problème noté sur 12 et quatre opérations notées sur 8 (avec souvent la preuve par 9 exigée). Lorsqu'on a supprimé l'examen, il fut remplacé par un dossier (Chemise rose pour les filles, bleue pour les garçons). Il comprenait outre le dossier et le livret scolaires, le cahier de compositions (CM1-CM2), renommé cahier de travail mensuel, mais sans classement.
Chaque mois, malgré les mathématiques modernes, on a continué à faire des problèmes de révision et ces fameuses opérations avec la preuve par 9. Cela a continué jusqu'en 1992. Les candidats disposaient de 20 minutes pour effectuer les opérations. Les élèves utilisaient les techniques opératoires traditionnelles françaises. Mais les pédagogues, aujourd'hui, reprochent à ces techniques d'être trop mécaniques. Vous trouverez une très bonne analyse à cette adresse:
Celle que j'ai toujours utilisée, du premier au dernier jour, est une méthode de cassage de la dizaine, et elle a l'avantage d'être plus rapide que la méthode de Singapour tout en suivant l'algorithme que tous mes parents d'élèves comprenaient. Ils pouvaient ainsi, aider leurs enfants. Comment font-ils aujourd'hui ? À Singapour, tout le monde parle le même langage mathématique. Démarche pédagogique On va organiser un jeu de rôle dans la classe. On utilisera des billets et des pièces factices. Les élèves seront, soit, l'oncle ou la tante, le neveu ou la nièce, le marchand ou la marchande, le voisin ou la voisine. On a vu un jouet dans la vitrine et le prix est affiché. L'oncle va l'offrir à son neveu. Il compte l'argent que contient son portefeuille. On entre dans la boutique. Malheureusement la marchande n'a pas de monnaie. L'oncle court chez la voisine et échange un billet de 10€ contre 10 pièces de 1€. (ou un billet de 100€ contre 9 billets de 10€ et 10 pièces de 1€ ou encore 10 billets de 10€. (suivant les données du problème). Maintenant, il peut payer le jouet et l'offrir à son neveu. On fait les comptes. Quelle somme d'argent reste-t-il à l'oncle ? Le but du jeu aura donc été de faire manipuler des billets et des pièces factices, de faire parler les enfants, et bien sûr, de comprendre le cassage de la dizaine ou (et) de la centaine qui mène à la technique opératoire.
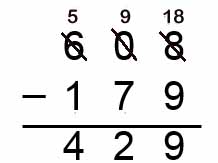
Technique opératoire On écrira la retenue de la ligne du haut, à gauche du chiffre des unités, et celle du bas, exactement, sous le chiffre de la dizaine, ou de la centaine. Les retenues du bas sont les billets donnés à la "voisine" sous le nombre de billets donnés à la "marchande". La retenue du haut, placée à la gauche, du nombre d'unités est la dizaine (10 éléments) qui résulte de l'échange (faire de la monnaie). 10 éléments + 2 éléments = 12 éléments. Dans le problème « Un oncle a dans son porte-monnaie 62€. Il offre à sa nièce un jouet valant 43€. Que lui reste-t-il ?» L'opération est 62€-43€=19€. L'oncle a donné à la marchande 3 pièces de 1€ et 4 billets de 10€. Il a donné 1 billet de 10€ à la voisine en échange de 10 pièces de 1€ (les retenues : "J'emprunte une dizaine et je la rends"). Il lui reste 1 billet de 10€ et 9 pièces de 1€. Chaque élément du problème de la soustraction est à sa place. Les enfants retrouvent donc les repères de la représentation spatiale qui les guideront dans le déploiement de l'algorithme opératoire. Cette méthode permet d'éviter l'écueil de la boîte noire; la différence de deux nombres ne change pas si on ajoute la même quantité à chacun des deux nombres; notion que trop peu d'élèves de cours élémentaire pouvaient comprendre clairement. Pour terminer, on effectuera la preuve de la soustraction. Evidemment, l'apprentissage est progressif. On ne passera aux nombres de 3 chiffres que lorsque la soustraction de nombres inférieurs à 100 aura été automatisée. On aura d'ailleurs commencé ce jeu du marchand ou de la marchande par des soustractions sans retenue. Peu à peu, on élude les phrases, et plus tard, au CM2, les bons élèves parviennent même à ne plus écrire de retenues du tout. C'est monsieur Roma, conseiller pédagogique de monsieur Magnan, qui m'a appris cette méthode, pour ma première classe, un CP-CE1, au retour du service militaire, en janvier 1965, en plein milieu de l'année scolaire. « Manipulations d'abord....et chaque chose à sa place...», répétait monsieur Roma, pour la soustraction, comme pour la division (alors au programme de CP). Aujourd'hui, après avoir vu la méthode de Singapour, je conseillerai de compléter par un schéma visuel représentant l'algorithme. Il faudrait aussi qu'il soit accessible très facilement. Certains pédagogues français prétendent que l'utilisation des pièces de monnaie nuit à la compréhension du nombre. Alors, comment se fait-il que les enfants de Singapour soient les meilleurs du monde à TIMSS ? Ouvrez le livre de CE1, de la page 43 à la page 47, et constatez. Cette hypothèse devient même ridicule quand on voit avec quelle facilité les petits bretons faisaient leur petites commissions. Relisez un petit passage du livre "Le cheval d'orgueil", de mon professeur respecté, Pierre-Jakès Hélias.  Voir ici. Voir ici.
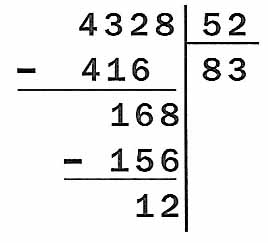
La soustraction est un élément de l'algorithme de la division. À Singapour, les traces du cassage des dizaines et des centaines qui prennent beaucoup de place au CE1, au CE2, et au CM1, disparaissent au CM2, dans la division. J'aimerais savoir quand et comment. Car ce qui faisait la force de la division traditionnelle française résidait en cette capacité d'abstraction et de calcul mental. Les très bons élèves n'écrivaient même pas la retenue, au CM2
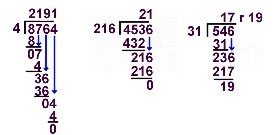 La division à Singapour Il est très difficile de traduire une méthode inconnue en France. Les soustractions et divisions traditionnelles françaises étaient les plus performantes. Il suffirait de savoir bien les enseigner ! |
 Primaths
Primaths