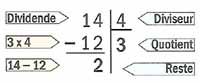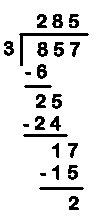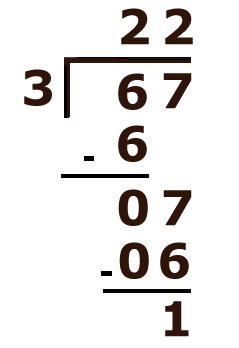Le but de la leçon est de faire comprendre toutes les lignes des tables par 7, la commutativité, en étudiant tous les problèmes ligne par ligne. L'élève devra donc manipuler, bien observer, dessiner, écrire ses résultats, sur son cahier. On veillera à ne pas faire provoquer d'erreur à l'oral. L'enfant exprimera, avec la précision du langage arithmétique, ce qu'il a vu et compris. (2 fois 3 œufs et 3 fois 2 œufs, par exemple, ce n'est pas exactement la même chose !)
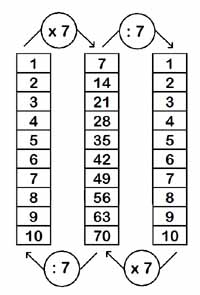
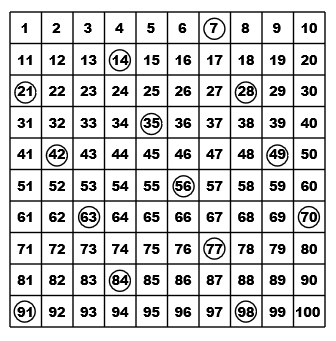
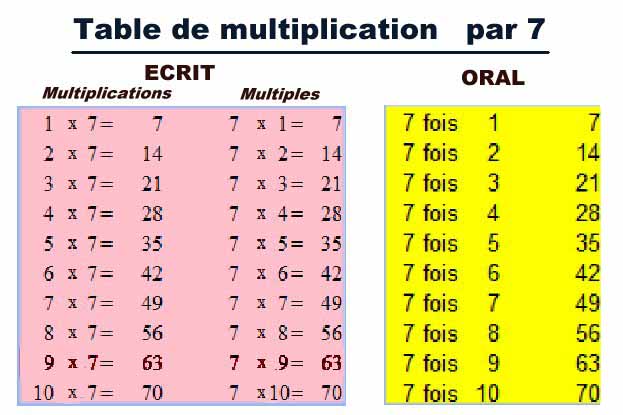
On commencera par faire établir la suite des nombres: 0 - 7 - 14 - 21 - 28 - 35 - 42 - 49 - 56 - 63 - 70
On fera lire et relire, oralement, ces lignes plusieurs fois afin de mémoriser les résultats de la table par 7.
Ces suites resteront affichées au tableau. On passera assez rapidement sur les 6 premières lignes des tables, car elles auront déjà été vues dans des leçons précédentes. On étudiera soigneusement les décompositions multiplicatives de (7 fois 7),(7 fois 8) et (7 fois 9). Le tableau mural sera divisé en quatre parties,
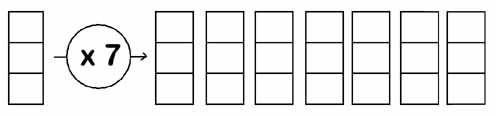
Je pose le problème: 7 poules vivent au poulailler. Chacune pond un œuf par jour dans son nid. Dessinez, à la craie, les nids sur vos tables, comme sur le tableau.
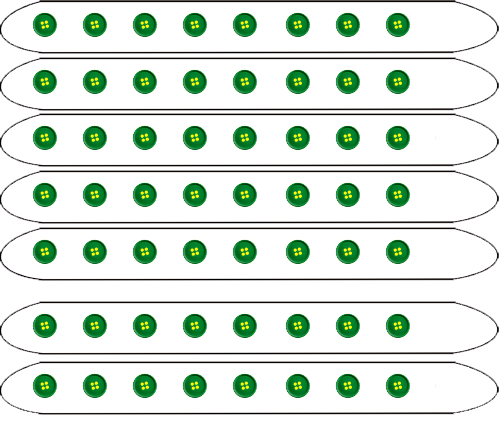
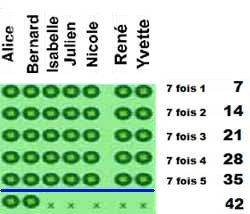
Un œuf sera représenté par un bouton. Faites pondre vos poules. Chaque enfant place un bouton par ensemble. Combien y a-t-il d'œufs en tout ? (1 + 1 + 1 + 1 + 1 + 1 + 1 = 7) soit 7 fois 1 7 (1 x 7 = 7) On fera répéter par les enfants 7 fois 1 7 et le maître écrira la ligne 1 x 7 = 7 au tableau.À la fin de la journée, on va récupérer nos œufs et les placer dans notre panier. Combien d'œufs a-t-on dans son panier ? Le maître représente l'ensemble de 7 œufs au tableau. Maintenant, pour porter les œufs, combien de fois devra-t-on se déplacer ? Avec combien d'œufs ? On fera répéter par les enfants 1 fois 7 7 et le maître écrira la ligne 7 x 1 = 7 au tableau.
Mais on décide de laisser les œufs en place, afin d'avoir plus tard des petits poussins. Alors, replacez ces œufs, chacun dans son nid. 2e jour: Les poules ont pondu chacune un 2e œuf. Placez vos boutons, et dites ce que vous voyez : (2 + 2 + 2 + 2 + 2 + 2 + 2 = 14) donc 7 fois 2 14 (2 x 7 = 14) Maintenant, vous allez dessiner des paniers, un par jour, et dessiner la récolte journalière. Que devez-vous dessiner ? Deux paniers contenant chacun 7 œufs Donc(7 + 7 = 14) donc 2 fois 7 14 (7 x 2 = 14) Le maître complète, (ou fait compléter le tableau mural par des élèves).
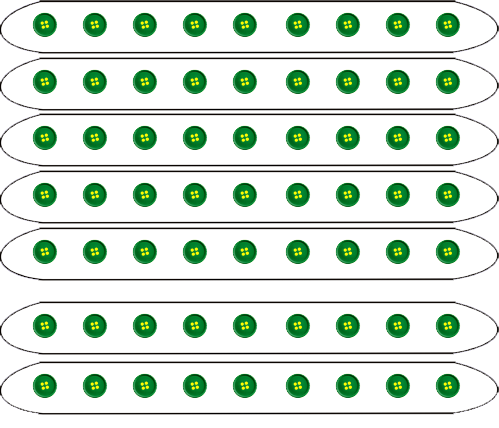
3e jour: Les poules ont pondu chacune un 3e œuf. On procède comme la fois précédente.
4e jour: Les poules ont pondu chacune un 4e œuf. On procède comme la fois précédente.
5e jour: Les poules ont pondu chacune un 5e œuf. On procède comme la fois précédente.
6e jour: Les poules ont pondu chacune un 6e œuf. On procède comme la fois précédente.
7e jour: Les poules ont pondu chacune un 7e œuf. On procède d'abord comme la fois précédente.
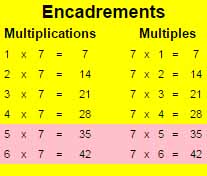
On va faire remarquer que les lignes des tables de multiplication et des tables des multiples sont identiques. On va maintenant demander aux enfants de déplacer les boutons, de les aligner afin de pouvoir observer une ou plusieurs décompositions multiplicatives, qu'ils écriront sur leur cahier. (Les séparations peuvent être matérialisées par des règles). En voici quelques unes :
8e jour: Les poules ont pondu chacune un 8e œuf. On procède d'abord comme la fois précédente.
(7 fois 8) ou (8 fois 7) sont les lignes que les enfants ont le plus de mal à mémoriser. Après les recherches des enfants, leurs manipulations, je ne vais retenir que 3 décompositions multiplicatives.
9e jour: Les poules ont pondu chacune un 9e œuf. On procède d'abord comme la fois précédente.
Après les recherches des enfants, leurs manipulations, je ne vais retenir que 3 décompositions multiplicatives.
Un truc de la table par 9 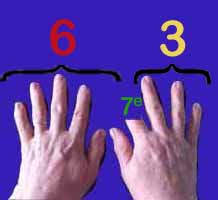
On remarquera aussi que 6 + 3 = 9 10e jour: Les poules ont pondu chacune un 10e œuf. On procède d'abord comme la fois précédente.
Mémoriser 7 fois 10 =70, ne présente pas de difficulté. L'enfant qui entre au CE2 devrait connaître parfaitement ses tables x5 et x2. Donc en utilisant les décompositions multiplicatives établies par les manipulations on pourrait aussi retrouver n'importe quelle ligne de la table par 7, car 5+2=7.
En résumé
Table des multiples
Table de multiplication
Ensuite on va faire lire à haute voix la table destinée à être apprise par cœur. On veillera à éviter autant que possible les erreurs de prononciation qui pourraient parasiter plus tard les réponses en calcul mental.
Je recommande d'exécuter ensuite, en fin de journée, ou le lendemain, des exercices, en utilisant le livre Techniques opératoires au cycle III (éditions Buissonnières à CROZON (29)
La table de multiplication apprise dans l'ordre va être lue, puis appliquée, dans le désordre.
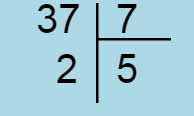
Avant, les exercices de divisions, il faudra rappeler la suite des nombres.
ou mieux
Remarques
Je viens de faire de mémoire une fiche qui ressemble à celle que j'ai utilisée pour la dernière fois, il y a plus de 20 ans déjà, et pour la première fois, en ... 1967. Donc, ici, je n'ai peut-être pas employé les mots justes. C'est, surtout, la démarche pédagogique qu'il faudrait retenir. C'est la démarche scientifique de la leçon d'observation des années 60. On apprend à l'enfant à observer dans le moindre détail, à provoquer sa curiosité, à exprimer ce qu'il voit, à le représenter, à mémoriser.
Cette fiche, je ne l'ai pas inventée. Avant 1970, l'Ecole Libératrice, revue du SNI (Syndicat national des instituteurs), publiait chaque semaine tout un fascicule de modèles de fiches pratiques. C'est là que je l'avais découverte. On fera remarquer que les nids sont plats (ligne horizontale) tandis que les paniers sont profonds (ligne verticale). Je ne suis pas allé, toujours, au bout de la fiche, faute de temps. Dans ma classe à plusieurs niveaux (CE2-CM1-CM2), il fallait avoir l'œil sur sa montre. Et il fallait abréger, préparer les exercices écrits. Alors, seuls les très bons élèves pouvaient retenir les algorithmes des opérations les plus difficiles qu'ils avaient découverts. Il ne suffit pas de trouver, ou surtout, de regarder ce que les autres ont trouvé, il faut aussi mémoriser. C'était difficile car je ne disposais pas d'un support visuel permanent de qualité. Mes petits programmes informatiques devraient permettre de résoudre ce problème, de poursuivre le travail ébauché et de consolider l'acquisition des automatismes. Mon programme d'entraînement (multi.htm) permet d'afficher à l'écran les principales décompositions. Par copie d'écran, impression, agrandissement à l'aide de la photocopieuse, on pourrait tirer des images pour un affichage mural. Ainsi, tous les élèves pourraient mémoriser intelligemment les lignes les plus difficiles des tables. Je ne connaissais pas le «truc» des mains. Merci à l'ami François qui me l'a appris récemment. Mais ce n'est qu'un «truc». Le soir, à la fin des classes, je demandais aux enfants de lire la table (avec le mot fois) avant d'aller au lit. Je leur précisais qu'ils seraient interrogés le lendemain, dans le désordre. Nous savions que le sommeil joue un rôle important dans la mémorisation, et que ce serait le schéma de chaque ligne qui serait mémorisé. Les enfants vont revivre les manipulations de la leçon. Aujourd'hui cette conviction est devenue une certitude.
Il faudra attendre les travaux de Karni et coll. (1994), puis ceux des équipes de Stickgold, Ribeiro, et Born, pour prouver que, sans aucun entraînement supplémentaire, les performances cognitives et motrices s'améliorent significativement et de façon durable après une période de sommeil, alors la perturbation du sommeil bloque sélectivement cette consolidation.
Le matin, les parents disponibles et consciencieux faisaient reviser la leçon à leur enfant, avant le départ pour l'école. Et moi, je n'avais qu'à contrôler... Le premier jour, le matin, j'utilisais le procédé Lamartinière. 5 petits problèmes et je donnais 10 secondes de réflexion avant de répondre. Dans la journée, je les faisais passer un par un à l'ordinateur (Voir mes programmes). Pas de limite de temps, mais il fallait tout de même répondre le plus rapidement possible. Les jours suivants je diminuais progressivement le temps de réflexion du procédé Lamartinière et je variais les méthodes d'interrogations, orales ou écrites, en alternant multiplications et divisions à reste nul. Plus tard, je passais à la division euclidienne avec reste non nul. C'est le fin du fin. Alors, on sait sa table de multiplication. Je ne pense pas avoir eu d'élèves particulièrement stressés. Et finalement, tous parvenaient à comprendre et mémoriser ces tables. Et ils les savent encore aujourd'hui, de nombreuses années après. SINGAPOUR
IMPORTANT !!!
Le livre de CE2 de Singapour dont je fais l'éloge est celui préfacé par le grand mathématicien Laurent Lafforgue. Une nouvelle version vient de paraître, une traduction américanisée qui ne tient aucun compte des particularités de la langue française.
Après les brillants résultats de Singapour à TIMSS 2015, j'ai eu la curiosité d'aller étudier leur méthode. D'abord, le livre de l'élève est l'outil qui aurait été parfait pour mes élèves. Les schémas à mémoriser sont les mêmes que les miens. Comme moi, ils font construire les 2 formes de tables (multiples et multiplications) simultanément. Les schémas de la multiplication sont les mêmes que ceux de la division.
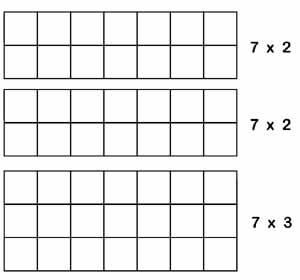
Mais, ils ne procèdent pas de la même façon. Tandis que moi, j'aligne les éléments un par un, à Singapour on présente d'abord le rectangle quadrillé. On découpe le quadrillage par bandes.
7 fois 3 ou 3 x 7 = 3 + 3 + 3 + 3 +3 +3 + 3 = 21 Cette présentation a l'avantage de prendre la commutativité d'emblée. La langue anglaise permet de faire lire 7 groupes de 3 : (7 x 3) au lieu de (3 x 7). Mais avec l'apprentissage simultané de la division et de la multiplication, l'opérateur des mathématiques modernes va permettre d'avoir une idée concrète des problèmes de vie courante.
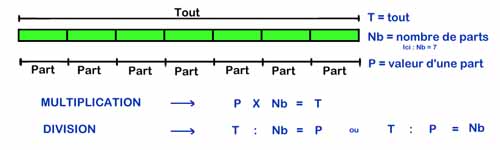
Mais voici le schéma qui est l'un des atouts de Singapour, pour résoudre des problèmes. Le même schéma sert à représenter la multiplication et la division
La représentation de la suite des nombres est également une ligne brisée.
La nouvelle représentation de Singapour après un transit aux USA. 
Tout un symbole. La calamité des premiers pas en mathématiques.
La disposition des nombres préconisée par la méthode de Singapour recommandée par Laurent Lafforgue est astucieuse. On voit très bien en bout de ligne, ce que l'on appelait autrefois la gare des dizaines. (10-20-30-40-etc ...)
On passe
Autrefois, c'est ce calcul que l'on faisait faire pour établir la liste des multiples de 7. Il ne nous serait jamais venu à l'idée de faire du comptage-numérotage. Comment voulez-vous qu'un enfant puisse trouver des repères dans cette file numérotée américaine ? Le tableau comprenant les gares des dizaines, permet d'aller bien plus loin que la table de multiplication, de jouer avec les nombres. On peut observer une disposition géométrique des nombres multiples de 7. Dans la suite de nombres matérialisée par la ligne (14 ... 98), quel sera le multiple suivant ? Cette suite de nombres est géniale: Elle utilise les compléments à 10 et les décompositions additives du nombre 7 (de 6 , 8 ou 9 pour les autres tables difficiles à mémoriser). Là, on joue avec les nombres. On ne numérote pas. Je ne connaissais pas cette méthode. On a toujours quelque chose à apprendre. Mais les "experts" français, eux, ils savent tout. Ils n'ont rien à apprendre des autres. Tout juste s'ils ne font pas la leçon aux pédagogues de Singapour. Si c'était à refaire, je fignolerais ma fiche en me servant des atouts de Singapour, et leur livre de CE2 est un véritable bijou. Les enfants de Singapour ont des schémas devant les yeux à chaque fois qu'ils ouvrent leur manuel !!! Je ne vais pas dire comment je procéderais exactement. Cela va faire plus de 20 ans que je n'ai pas eu d'élèves. Mais je n'oublierais pas qu'en France on parle Français et qu'à Singapour on parle quatre langues, l'anglais, le mandarin, le malais, le tamoul. À l'école, les cours se font en anglais. D'où l'importance des schémas. Mes premiers élèves n'avaient que les traces laissées sur le cahier de brouillon comme aide visuelle permanente. Donc seuls les très bons élèves mémorisaient les schémas les plus difficiles. Les autres devaient retenir bêtement une dizaine de lignes sur une centaine. Le livre de Singapour permet à tout le monde d'avoir en mémoire ces algorithmes difficiles. Un grand merci aux pédagogues de Singapour ! Maintenant, je n'oublierais pas un affichage mural. Mais c'est trop tard, malheureusement. " J'entends et j'oublie, je vois et je me souviens, je fais et je comprends " De cette vieille maxime pédagogique chinoise, les pédagogues français ne retiennent que le verbe entendre, tandis qu'à Singapour, ce sont les verbes faire et voir qui ont la priorité. Et c'est bien là le drame français. Les enfants qui apprennent les automatismes dans une langue différente de leur langue maternelle ou qui n'ont pas un vocabulaire très riche, ou qui ont une lecture hésitante, sont pénalisés. À Singapour, la priorité donnée aux schémas visuels permet de réduire les barrières linguistiques et sociales. J'émettrais une réserve sur le livre de CE1. Peut-être convient-il dans un cours unique ? Ce dont je suis certain, c'est que je n'aurais pas pu l'utiliser dans ma classe (CE1-CE2-CM1-CM2). Je n'aurais pas pu faire lire 2 x 3, deux fois trois, tandis qu'au CE2 et au CM, j'étais un maniaque de 3 fois 2, pour la compréhension des problèmes (la place de l'opérateur). La traduction du livre de CE1 ne devrait-elle pas être revue, afin d'être adaptée à la langue française ? Mais pour mieux comprendre comment on mémorise verbalement les tables de multiplication à Singapour, le mieux est d'aller à la source elle-même,  à Singapour. à Singapour.
On peut aussi y découvrir d'autres astuces pour une mémorisation plus abstraite de certaines tables. Par comparaison, voici les suites que je proposais :  Voir Voir
Nul ne détient à lui seul toute la vérité. J'ai encore beaucoup de choses à apprendre. Une controverse fait rage en France sur l'apprentissage de la division. Il ne faut pas confondre division et technique opératoire de la division. N'étant pas un spécialiste, ni du CP, ni du CE1, je me garderais bien de commenter. À Singapour, ce n'est qu'au CE1 qu'apparaît le signe de la division en ligne :
Toutes les divisions, au CE1, ont un quotient inférieur à 10, un reste nul. Elles complètent l'apprentissage d'une table de multiplication (2, 5, 3, 4 et 10). La potence, c'est au CE2, à partir de la page 57, avec d'ailleurs une erreur de traduction (Quotient et retenue). Moi, j'aurais écrit reste au lieu de retenue. L'apprentissage est progressif. On ne trouve aucun diviseur supérieur à 10 dans le livre de CE2. Les diviseurs de 2 chiffres, c'est au CM2.
Dans la nouvelle version du livre de la librairie des écoles, la première potence, c'est (82:4) à la page 92. On met la charrue avant les bœufs.
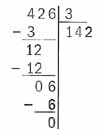
Cette technique opératoire fait suite à l'apprentissage des tables de multiplication, alors que dans le livre préfacé par Laurent Laffforgue, elle les précédait. Cela permettait d'avoir une potence pour un quotient à un chiffre, de verbaliser la procédure de la division et de mémoriser les tables. Dans la langue française, on a besoin de la table de multiplication et de la table des multiples pour comprendre le sens concret de chaque problème posé. Cette américanisation du calcul est une grosse faute pédagogique. Progression à Singapour, livre de Laurent Lafforgue (dès la page 57 du manuel de l'élève ) au CE2: À Singapour, on pose la soustraction. L'enfant n'a donc pas à garder en mémoire tout le contenu de la soustraction. L'algorithme est matérialisé. (9:2); (12:2) (28:2); (34:2); (73:2) (400:2); (500:2); (550:2); Révision des tables par 3; 4; 5 (96:4); (80:3); (426:3); (823:4) Ce n'est qu'ensuite qu'on procédera à des divisions par 6;7;8;9 au moment de l'apprentissage de ces tables de multiplication. Avant 1970, en France, tel que je l'ai fait, on posait une potence dès le CP. Mais pouvait-on vraiment parler de technique opératoire ? Cette potence permettait surtout à l'enfant à se repérer dans l'espace. Chaque élément devait être à sa place. Le plus important, au cours élémentaire, à Singapour, comme dans la méthode de l'école libératrice, ce sont les schémas qui servent aussi bien pour la multiplication que la division. Donc l'enfant comprend simultanément le sens des problèmes de multiplications et de divisions. Apprendre les opérations les unes après les autres est donc une progression rétrograde. Voilà comment les petits Français prennent trois années de retard sur les petits Singapouriens. La page 70 du manuel de CE2, première leçon des tables de multiplication, me rappelle mon Postel des années 70. La machine multiplie le nombre qu'on donne par 6. La machine divise le nombre qu'on donne par 6. Le chapitre 6, page 106 est consacré au calcul mental. Ce ne sont pas les mathématiques du 19e siècle. À Singapour, on se sert d'opérateurs (les machines) qu'on décompose ou qu'on réduit. Les chaînes d'opérateurs, en résolution de problèmes, c'est la programmation informatique sans ordinateur. L'opérateur n'est qu'un élément d'une opération. Une chaîne est un algorithme. La comprendre, c'est être capable de la décomposer, puis de la recomposer. Cet algorithme peut être traduit et écrit dans un langage de programmation informatique pour être exécuté par un ordinateur. Les enfants de Singapour se préparent aux progrès techniques du 21e siècle. En nous servant des atouts des uns et des autres, la France pourrait retrouver son niveau d'antan. Mais cela ne sera possible que le jour où les chercheurs français feront preuve d'humilité et acceptent de se remettre en cause. Pourquoi ne font-ils pas l'effort de recherche que j'ai fait à mon petit niveau ? | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
































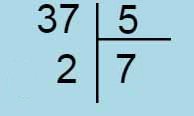
 Voir ces programmes
Voir ces programmes