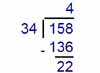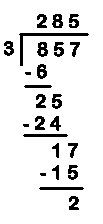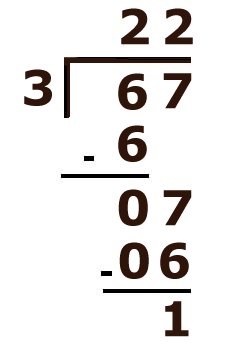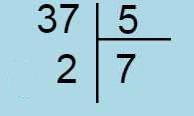C'est largement suffisant pour apprendre la mécanique opératoire et il ne s'agit pas de gaver un enfant d'un nombre inconsidéré d'opérations. Au départ, une suite de 3 opérations suffit. Mais les enfants prenaient cet exercice pour un jeu, et j'étais bien obligé de leur proposer plusieurs courses.
Attention, il ne faut pas utiliser mon solveur de divisions, n'importe comment. Il faut s'en servir intelligemment:
On construit un automatisme à partir d'un algorithme que l'on comprend.
J'ai enseigné assez longtemps le tennis de table pour savoir qu'un geste technique, d'abord, on le prépare, jeu à blanc, par exemple, ou par imprégnation en faisant observer un joueur à la technique parfaite. Lorsque ce geste technique est plus ou moins acquis, on va le fixer par des exercices répétitifs, en utilisant un robot lanceur de balles, ou des paniers de balles. Si on automatise un mauvais geste, cela peut devenir catastrophique, car il peut se transformer en réflexe qu'on ne parviendra que très difficilement à perfectionner. Il restera toujours des mouvements parasites qui contrarieront la progression de l'élève.
Mais l'utilisation rationnelle du robot peut remplacer de façon profitable les longues et ennuyeuses séances de travail en régularité.
Pourquoi serait-ce différent en calcul mental et en techniques opératoires ? Mêmes causes, mêmes effets.
Il faudra attendre les travaux de Karni et coll. (1994), puis ceux des équipes de Stickgold, Ribeiro, et Born, pour prouver que, sans aucun entraînement supplémentaire,
les performances cognitives et motrices s'améliorent significativement et de façon durable après une période de sommeil, alors la perturbation du sommeil bloque sélectivement cette consolidation.
 Cours de Stanislas Dehaene au Collège de France
Cours de Stanislas Dehaene au Collège de France
La technique de chaque type de divisions aura été préalablement découverte, ou expliquée de façon conventionnelle, mais comprise. Ce n'est qu'ensuite que l'élève pourra venir s'entraîner sur des opérations qu'il aura d'abord réalisées sur papier, si possible à partir d'un problème. Refaire un même problème avec des données différentes, permet d'automatiser un algorithme de résolution, donc de créer une image mentale. Il faut suivre une progression par ordre de difficultés, celle des vieux manuels de calcul, par exemple, et proposer des exercices similaires.
L'observation de l'arborescence de mon programme vous permettra de découvrir les sept étapes que je préconise.
Evitez la "progression" des livres les plus utilisés aujourd'hui au CE2. La première fois qu'ils divisent avec une potence, c'est (67:3), page 129 pour le premier. Le second est encore plus optimiste (857:3) page 117. Ils ignorent la représentation spatiale, les repères que la potence peut fournir aux enfants.
Les écritures algébriques (22 x3) + 1 ou (285 x3) +2, que certains privilégient, c'est, tout simplement, la vérification de la division euclidienne. C'est abstrait. q=? et r=? , c'est mieux. Mais sans potence, cela demeure abstrait. Où, dans quel espace, l'enfant situe-t-il D et d ? Et ils mettent, encore, la charrue avant les bœufs. On fonce au fond du puits sans prendre le temps de comprendre le rez-de-chaussée.
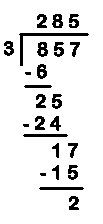
|
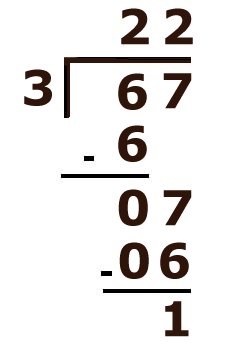
|
|
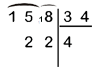
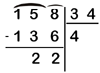
Représentation spatiale à Singapour.
|
Êtes-vous capable de comprendre ces opérations ?
Mettez-vous à la place d'un enfant de huit ans qui, en France, doit résoudre ces opérations, le jour où il voit une potence pour la première fois.
Ignorance, ou sabotage des programmes de 2008 ? Comprendre un algorithme, c'est savoir le décomposer !
Je trouve aberrant que les formateurs français abordent la multiplication et la division par deux voies intellectuelles différentes et séparément, l'une après l'autre.
Pour la multiplication, ils placent indifféremment les deux facteurs par rapport au signe x. Donc, les enfants ne voient pas les deux sens différents des problèmes.
Par contre, ils attachent une énorme importance aux deux sens (partition et quotition) de la division, ce qui entraîne le report de l'apprentissage des techniques opératoires à plus tard, des techniques parfois farfelues en terme de rapidité calculatoire.
À Singapour, comme dans ma méthode de « L'école libératrice », on fait très attention à la position de l'opérateur dans la multiplication ce qui permet de bien comprendre les problèmes multiplicatifs. Pour la division, c'est par la preuve, la commutativité de la multiplication, que l'on peut introduire très tôt la technique opératoire. Les deux sens (quotition et partition) sont compris beaucoup plus facilement car les enfants apprennent simultanément les tables de multiplication et de division. Ils comprennent plus facilement les problèmes, car ils reposent sur des petits nombres qu'ils peuvent manipuler concrètement. Les schémas de la multiplication et de la division sont les mêmes.
Pour être clair, je recommande, pour commencer, le programme suivant :
 Apprentissage des tables de multiplication et de division
Apprentissage des tables de multiplication et de division
Vous pouvez télécharger une version simplifiée (JavaScript)  ici
ici
Cette première marche est primordiale, capitale. Il ne faut pas la rater. Elle détermine toute la suite, que l'enfant sera à l'aise ou non, en calcul. Si l'enfant persiste à échouer, on le fera manipuler, schématiser. Il doit parvenir au calcul abstrait en le comprenant. C'est ici que l'enfant s'approprie les différents sens de la division (quotition, partition).
On a de meilleurs repères dans son jardin que dans l'océan.
 Voir des exemples de petits problèmes
Voir des exemples de petits problèmes
|
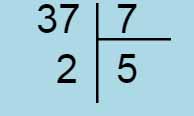
On peut permuter le diviseur et le quotient
(commutativité de la multiplication)
dans la preuve de la division.
|
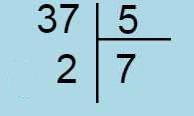
|
|
( 5 x 7 ) + 2 = ( 7 x 5 ) + 2 = 37
Dans la division partition, 37 est le tout, 7 le nombre de parts, 5 la valeur d'une part et 2 le reste.
Grâce à la commutativité ( 7 fois 5 égale 5 fois 7), dans la division quotition, la valeur d'une part devient le diviseur.
On pourra donc appliquer la même technique opératoire pour les deux formes de divisions.
Cette manipulation permet de débloquer le report de la technique opératoire à la Saint-Glinglin.
Les quatre emplacements dans la potence sont des repères spatiaux.
C’est par les manipulations et leurs représentations, lors de l’apprentissage des tables de multiplication, que les enfants vont comprendre les divers sens de la division. Importante la vérification de la division !
Les pédagogues français qui se croient les meilleurs du monde ne veulent pas reconnaître leur ignorance ! Tous bâclent l'apprentissage des tables de multiplication !
Dans la nouvelle version du livre de la librairie des écoles, la première potence, c'est (82:4) à la page 92. On met la charrue avant les bœufs.
Cette technique opératoire fait suite à l'apprentissage des tables de multiplication, alors que dans le livre préfacé par Laurent Laffforgue, elle les précédait. Cela permettait d'avoir une potence pour un quotient à un chiffre, de verbaliser la procédure de la division et de mémoriser les tables. Dans la langue française, on a besoin de la table de multiplication et de la table des multiples pour comprendre le sens concret de chaque problème posé. Cette américanisation du calcul est une grosse faute pédagogique.
|
Éviter de brûler les étapes.
Le monde ne s'est pas fait en un jour.
Lorsque ce travail a été fait consciencieusement, on proposera des divisions où le quotient comporte 2 chiffres, puis 3, puis 4. Quelques séances suffisent. Je ne vois pas où est la difficulté qui a poussé les professeurs des écoles à demander le report de cette technique opératoire au CM1. Pas étonnant que la France soit lanterne rouge au classement Timss 2015.
J'étais en parfait accord avec la préface de "J'apprends les maths" de Rémi Brissiaud. Il est dommage qu'il n'ait pas maintenu cette conviction.
Deux chiffres au diviseur, c'est plus délicat. Singapour l'évite (Diviseur à 1 chiffre au CE2, division décimale et nombres complexes au CM1 et enfin, diviseur à 2 chiffres au CM2). Mais avant 1990, les petits Français étaient les meilleurs, grâce à notre division traditionnelle dès le CE2, méthode inconnue à Singapour.
On commencera là aussi avec un chiffre au quotient.
Le diviseur sera 20, 30 , 40, ... un nombre exact de dizaines. Ensuite on essaiera avec 21, puis des nombres de 2 chiffres en s'assurant qu'on n'a pas besoin de tâtonner.
Ce n'est que lorsque cet algorithme est automatisé que l'on passera à plus difficile (diviser par 37, par exemple).
Enfin, on procédera de la même façon pour passer progressivement à des quotients à 2, puis 3 chiffres.
Évidemment, chaque division aura été préparée par des problèmes concrets, des manipulations (voir les livres anciens).
J'organisais des courses. Les enfants devaient résoudre trois divisions l'une après l'autre. Lorsque la première était terminée, on me la montrait. Si c'était bon, on passait à la suivante. Sinon, l'enfant allait à l'ordinateur et utilisait le robot pour corriger, puis il reprenait la course.
À la fin, ceux qui avaient tout réussi, aidaient les retardataires à jouer avec le robot.
Mon solveur de divisions permet d'afficher de l'aide, tables de multiplication, etc. L'enfant ne sera pas en situation d'échec. Il pourra même afficher la solution, puis la masquer,... la revoir, ... Je recommande de faire lire à haute voix les phrases qui constituent l'algorithme de l'opération. Il répétera ainsi, sans erreur, très souvent, des séquences de tables de multiplication qui se graveront de façon définitive en mémoire et il s'imprégnera de l'algorithme de la division. La mémorisation verbale est excellente pour provoquer de bons réflexes
La table du diviseur (nombres de 2 chiffres) est intéressante pour apprendre à l'enfant à raisonner et trouver le quotient par encadrements. Il développera ainsi une forme d'intuition. La table de multiplication du diviseur lui permettra de trouver ses repères, si besoin. Mais c'est mieux quand on peut l'éviter (recherche dichotomique par tâtonnements).
Je donne la solution pour les deux types de divisions les plus utilisées. Je n'ai pas retenu les divisions par soustractions successives ou d'autres techniques, qui peuvent peut-être aider à la compréhension, mais qui font surtout perdre du temps et les bons repères.
 Pour information
Pour information
J'ai imaginé le solveur, avec réponses pas à pas, pour une verbalisation des actions effectuées, surtout, pour la division traditionnelle française car, c'est selon moi, celle qui permet de mieux progresser en calcul mental.
La division proposée au choix B est celle qui permet de mieux comprendre l'algorithme de la division.
Je ne détaille ni la multiplication, ni la soustraction au choix B. Ecrire de droite à gauche dans un formulaire est plutôt compliqué. Et si on devait donner le résultat chiffre par chiffre ce serait plus long et compliquerait l'algorithme.
Evidemment, au fur et à mesure des progrès, l'enfant se dispensera d'utiliser les aides, puis il n'aura plus besoin de mon robot. L'élite de la classe ne se servira de mon solveur qu'épisodiquement. Même les meilleurs font des erreurs de calcul. Ils retrouveront précisément l'endroit où l'erreur a été commise. Lorsque les erreurs deviennent rares, c'est que l'algorithme de la division est bien ancré en mémoire. On pourra dès lors utiliser une calculatrice. C'est une faute pédagogique que de faire utiliser une calculatrice par un enfant qui ne maîtrise pas l'algorithme opératoire et c'est l'inciter à une paresse intellectuelle. Une calculatrice est une boîte noire qui ne donne que le résultat (décimal) de la division (lorsqu'elle ne connaît pas la division euclidienne). Absence totale d'images mentales. Un ordinateur ne connaît que le code binaire (0 et 1). Mais lorsqu'il est correctement programmé, il peut remplacer avantageusement le maître pour des exercices répétitifs. Il est infatigable. Il ne gronde pas. Il ne s'énerve jamais. Il ne prononce pas de paroles malencontreuses susceptibles de stigmatiser l'enfant. Et ici, l'enfant parvient toujours au bon résultat tout en s'empreignant de l'algorithme que ne lui fournit pas une calculatrice.
Apprendre la technique opératoire de la division était chronophage.
Pourquoi était-ce long et difficile ? Tout simplement, parce que les élèves les plus faibles, n'ayant pas encore tout à fait acquis les automatismes de calcul, (tables, soustractions) se perdaient dans le cheminement vers le résultat. C'était un cercle vicieux.
Mon programme permet de séparer les difficultés. Le plus important, c'est l'algorithme. On utilise les aides calculatoires à bon escient.
En France, on a fait le choix de la médiocrité, reporter ce qui est difficile à plus tard en étalant les difficultés dans le temps. Mon robot, c'est l'inverse. Des exercices concentrés, intenses, mais brefs. On apprend le geste technique de la recherche dichotomique sans faute, dans un temps réduit. Et ainsi, on préserve le perfectionnement dans l'avenir.
Quand les programmes scolaires seront plus ambitieux, c'est à dire à la Saint-Glinglin, peut-être pensera-t-on à mon idée du robot qui ne demande qu'à être amélioré.
Une toute petite lueur d'espoir
 Les neurosciences pour lutter contre l'échec scolaire
Les neurosciences pour lutter contre l'échec scolaire
Dans le domaine de l'éducation, les enseignants doivent maintenir un haut niveau d'attention chez l'élève en stimulant, en rendant le cours attractif et en concentrant l'élève sur une seule tâche.
L'ensemble de l'article, c'est l'apologie de l'enseignement que j'ai essayé de mettre en pratique tout au long de ma carrière.
Mon robot date de 1997. La première version avait été écrite en Qbasic, compilée par Quickbasic.
Autrefois, tout exercice donné devait être corrigé. On utilisait surtout le temps qui devait être consacré à l'éducation physique, en fin de journée, pour procéder à des exercices répétitifs (BLED, Tables..etc.). Le mauvais temps avait bon dos... Et les parents finissaient le travail à la maison...
Un bon programme informatique permet à l'enfant une auto-correction. J'ai apprécié l'usage de mes quatre ordinateurs, surtout, lorsque j'avais une classe à 4 cours (CE1-CE2-CM1-CM2), où les corrections étaient interminables.
Les parents ne connaissent pas forcément la méthode utilisée à l'école. Depuis l'introduction des calculatrices, on n'enseigne plus beaucoup la méthode traditionnelle française (choix A), et certains ont du mal à s'adapter à la nouvelle (choix B) moins performante en rapidité, mais à l'algorithme plus clair. Maintenant, ils pourront aider leurs enfants s'ils utilisent aussi mon solveur de divisions.
Important:
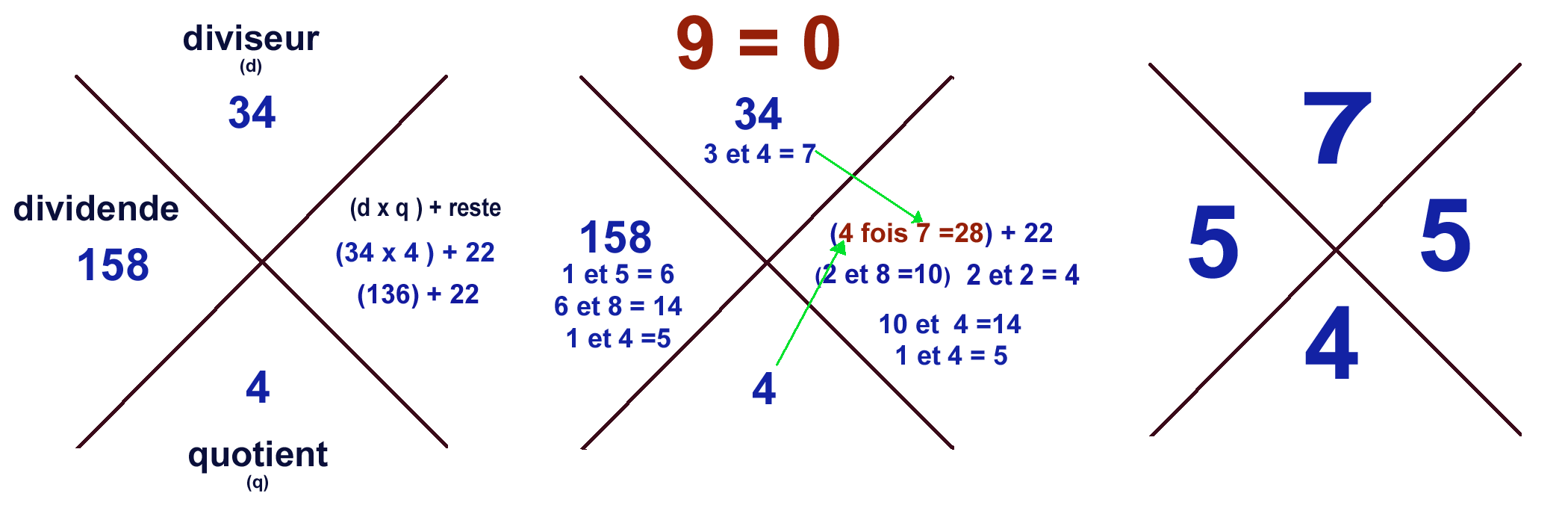
C'est la vérification manuelle de la division qui va éclairer le sens de l'opération dans le problème posé.
On peut permuter le quotient et le diviseur grâce à la commutativité de la multiplication.
( 34 x 4 ) + 22 ou ( 4 x 34 ) + 22 = 136 + 22 = 158
Autrefois la preuve par 9.
Attention :
Si le chiffre de gauche (5) est différent du chiffre de droite (5), alors, il y a erreur.
Mais l'égalité des 2 nombres ne garantit pas la justesse du résultat, car pour la preuve par neuf, 9=0.
J'ai écrit un programme identique en JavaScript, directement utilisable sur n'importe quel ordinateur, ou sur une clé USB.
Vous pouvez  télécharger l'application avec preuve par 9
télécharger l'application avec preuve par 9
Distribuez la sans modération aux enfants qui éprouvent des difficultés à apprendre l'algorithme de la division et leurs tables de multiplication qu'ils retrouveront dans les fichiers d'aide. Mais, pas plus vite que la musique !
Le fichier que vous lisez ne contiendra que l'essentiel.
Chaque enseignant pourra utiliser mon solveur selon ses convictions pédagogiques.
 télécharger, ici, l'application sans la preuve par 9 (JavaScript)
télécharger, ici, l'application sans la preuve par 9 (JavaScript)

 télécharger, ici, l'application de divisions de nombres complexes (JavaScript)
télécharger, ici, l'application de divisions de nombres complexes (JavaScript)